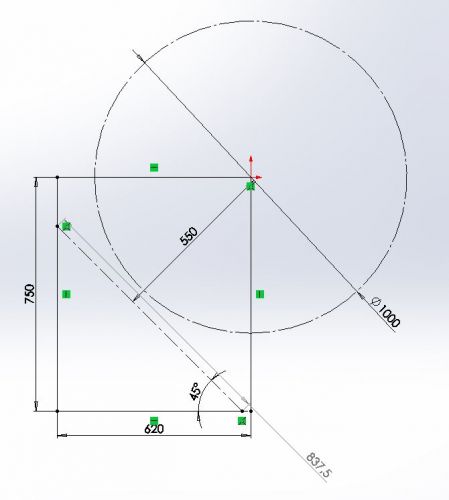
Dobrý den, prosím o radu pro výpočet přepony trojúhelníku viz. obrázek. Už si nevím rady...
V obrázku je hodnota, kterou potřebuji dopočítat šedivá. Děkuji Burián
2x
Možná to lze spočítat použitím vzorců z analytické geometrie. Zvolit např. střed kruhu jako střed souřadné soustavy. Jestliže ta úsečka, jejíž délku potřebujete spočítat, je pod úhlem 45 stupňů, tak vímě vektor ležící na dané úsečce.
Vímě, ža na té úsečce je bod, vzdálený od středu kruhu 550 mm. Tedy lze sestavit parametrické rovnice dané úsečky.
Lze taky sestavit parametrické rovnice těch dalších dvou úseček . Nálsedně je potřeba, spočítat průsečíky, a tedy zjistit souřadnice krajních bodů dané úsečky. Dle vzorce pro vzdálenost bodů následně lze spočítat délku.
Teď se mně to počítat nechce. Jsou zápasy ligy mistrů. Můžu to zkusit zítra, jestli se tak opravdu dá zjistit ta délka.
2x
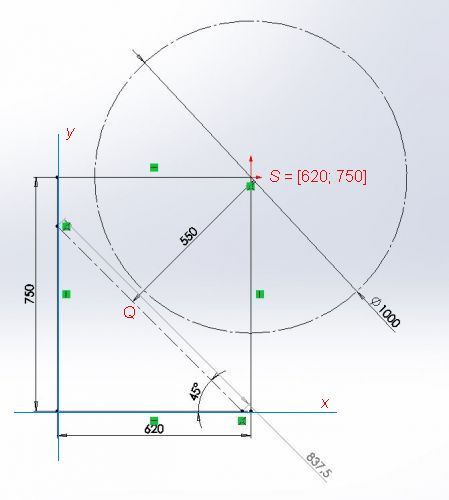
Než jsem vytvořil zápis, tak již je tu řešení od @lopezze. Já jsem umístnil počátek souřadnicového systému do dolního levého rohu obdélníka.
.
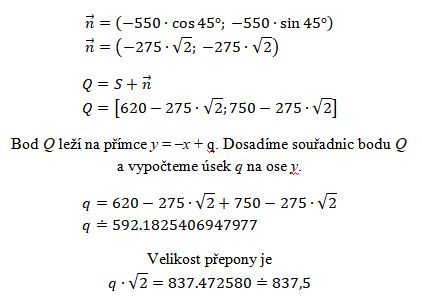
0x
Jestli tomu rozumím, na obrázku je pravoúhlý trojúhelník s úhlem 45° a přilehlou odvěsnou 620.
Pak cos(45°) = 620/p, což ale vychází p = 876,8.
Lze to vypočítat i pomocí Pytgahorovy věty.
Zdravím a nesouhlasím. Podle obrázku těch 620 není odvěsna zkoumaného trojúhelníka. Jeho odvěsna je "o kousek" kratší...
0x
Tohle není úkol do školy, ale něco z praxe. Problém je v tom, že řešíme trojúhleník D,E,F, jehož vztah k trojúhelníku A,B,C není znám a víme o něm jen to, že jeho výška je 550 (asi milimetrů). Kružnice průměr 1000 nám je k ničemu (já mám nakreslenu R=550, na tu je to alespoň tečna). Takže vypočítat to podle mě nejde, jen mě mate, že zkonstruovat to jde.
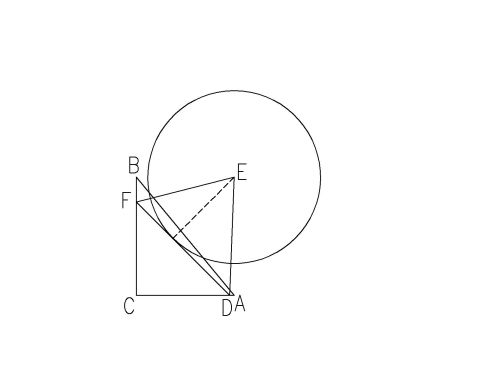
Zdravím.
Tohle je ale jiný příklad než ten v dotazu. Zde: "... já mám nakreslenu R=550, na tu je to alespoň tečna..." - z toho plyne, že "čárkovaná" je kolmá na DF (tečna s poloměrem)...
0x
Když je střed souřadné soustavy ve středu kruhu, tak
rovnice vodorovné úsečky je
y = - 750
rovnice svislé úsečky je
x = - 620
K bodu [0;0] "přičíst" vektor (- odmocnina ze 151250; - odmocnina ze 151250) tedy přibližně vektor (- 388,9 ; - 388,9)
Tedy na dané úsečce je bod [ - 388,9 ; - 388,9]
Parametrické rovnice dané úsečky jsou
x = - 388,9 + t
y = - 388,9 - t
--------------------
Dosadit za y hodnotu -750
- 750 = - 388,9 - t1
t1 = 361,1
x = - 388,9 + t1 = - 27,8
Souřadnice jednoho krajního bodu je [ - 27,8 ; - 750]
------------
Dosadit za x hodnotu - 620
- 620 = - 388,9 + t2
t2 = - 231,1
y = - 388,9 - t2 = - 620
Souřadnice druhého krajního bodu je [ - 620 ; - 157,8]
Vzdálenost je odmocnina z [(-620 + 27,8)2 + (-157,8 + 750)2] = odmocnina ze 701402 což je 837,5
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.