Dobrý den, chtěla bych se zeptat, pomocí jakého postupu můžu z obecné rovnice:
přímka q: x+3y-3=0 udělat rovnice parametrické, tedy x=... a y=...
Děkuji za odpověď
4x
Např. za y zvolíme 1 a dostaneme x = 0. Tudíž získáme bod A = [0; 1]. Směrový vektor je u = (3,-1), tj. kolmý k vektoru normálovému, jak uvedl @kartaginec. Takže stačí již jen dosadit do parametrického vyjádření přímky
X = A + tu, t∈ R:
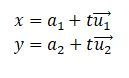
4x
vzorec obecné rovnice přímky je:
ax + by + c = 0
a, b jsou souřednice normálového vektoru dané přímky (tedy vektoru kolmého na přímku)
------
Příklad, který jste napsla, je takto:
q: x+3y-3=0
před x není číslo, takže je to 1
před y je 3
Tedy normálový vektor přímky q je n(1;3)
V parametrických rovnicích je použit směrový vektor, který je rovnoběžný s přímkou (tedy je kolmý na normálový vektor)
Směrový vektor vytvoříme tak, že prohodíme souřadnice normálového vektoru a u jedné z nich změníme znaménko.
Směrový vektor označím např. u
u (-3;1)
Aby bylo možné napsat parametrické rovnice, potřebujeme souřadnice nějakého bodu, který leží na dané přímce.
Je jedno, který je to bod. Tedy jednu souřadnici bodu zvolím a druhou dopočítám. Zvolím např. x = 1
Dosadím 1 za x do obecné rovnice a dopočítám y.
1+3y-3=0
3y = .2
y = 2/3
Tedy bod [1;2/3] je na přímce q.
První souřadnice toho bodu (tedy 1) je v první parametrické rovnici.
Druhá souřadnice toho (tedy 2/3) bodu je v druhé parametrické rovnici.
Výsledné rovnice parametrického vyjádření přímky q jsou:
x = 1 - 3t
y = 2/3 + 1t
Za souřadnicí směrového vektoru je t, protože za t lze dosazovat čísla a počítat tak souřadnice dalších bodů na přímce.
doplněno 10.11.20 13:03:
oprava : a,b jsou souřadnice ...
doplněno 10.11.20 13:04:
Tady je odkaz na soubor, kde je to znázorněno
4x
Když už jsou tu ty postupy s normálovým vektorem rozebrány, podívejme se na druhou možnost – vyjít ze dvou bodů přímky. V našem případě mohu třeba položit x = 0 a dostanu 3y-3=0 a tedy y = 1; násůedně položřím y = 0, odkud vyjde x = 3. Mám tedy dva body M = M[0;1], N = N[3;0]. Rozdíl těchto bodů u = N-M je pak směrový vektor u = u(3;-1) (jedna z možností).
Další postup je pak stejný, jako když jsme vyšli z normálového vektoru.
2x
To jde různě. Vpodstatě potřebujete znát směrový vektor, což je kolmý k normálovému vektoru (1;3), a jeden bod přímky. Také můžete najít dva body přímky, odkud také získáte směr.
2x
Jiný příklad na totéž:
p: 3x + 2y -3 = 0
n (3 ; 2)
Prohodit čísla a u jednoho z nich změnit znamínko
Vznikne směrový vektor
u (2; -3)
Zvolit za x nějaké číslo, třeba 2
3 krát 2 + 2y - 3 = 0
2y = -3
y = -3/2
Bod , např. A, ležící na zadané přímce je
A [2 ; -3/2]
Výsledné vyjádření parametricky je:
x = 2 + 2t
y = -3/2 -3t
Musí tam být to t, v obou parametrických rovnicích
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.