Díky za jakoukoli pomoc.
0x
Kvadratická rovnice jistě může být, Ale spíš mi to připadá výpočet minimální vzdálenosti "s" v závislosti na proměnné "t" dle rovnice
s²=((5t-800)/t)² + (900/t)²
Vyjádřit "s", zderivovat, rovnici položit =0. Dostaneme čas a již můžeme spočítat, jak jsou letadla od sebe vzdálená v čase "t", což může být minimální, ale taky maximální vzdálenost
Existuje ještě možnost, pokud tazatelka nezná integrální počet, zvolit za s=3,5 a spočítat zda má rovnice řešení pro "t" v oboru reálných čísel
12,75t²-8000t+1450000=0
V tomto příkladě lze derivací zjistit minimální vzdálenost.
Maximální vzdálenost závisí např. na tom, kam daná letadla letí a v jaký čas bychom tu vzdálenost vyhodnocovali ![]()
Funkce vzdálenosti v závislosti na čase a její následná derivace kdy hledáme čas v kterém je směrnice tečny ke grafu funkce rovna nule, je běžný postup. Otázka je, zda tazatelka má řešit příklad a je již vybavena těmito znalostmi.
Myslím, že pokud sestavená rovnice nemá řešení pro čas "t" v oboru reálných čísel pro vzdálenost 3,5 km, že je podmínka zadání taky naplněna.
0x
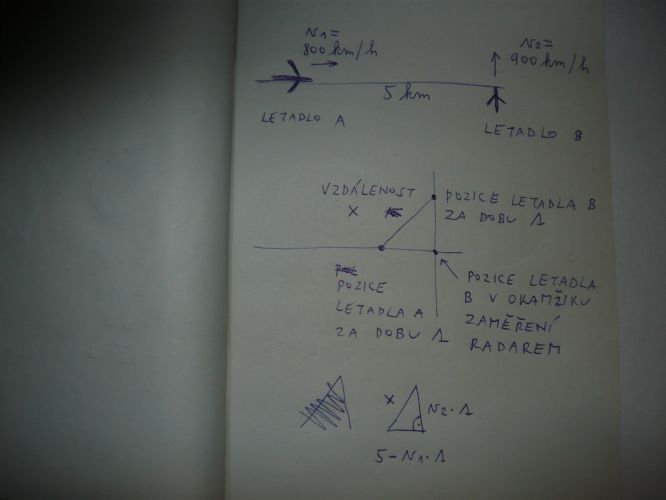
V přiložené fotce je náčrt vzájemné pozice letadel.
x ... okamžitá vzdálenost mezi letadly
x lze vyjádřit pomocí pythagorovi věty
x2 = (5 - v1 krát t)2 + (v2 krát t)2
x = odmocnina z [(5 - v1 krát t)2 + (v2 krát t)2]
Dosazení hodnot rychlostí
x = odmocnina z [(5 - 800 t)2 + (900t)2]
minimální hodnotu x lze zjistit zderivováním
doplněno 06.11.20 20:08:
x = odmocnina z [25 - 8000 t + 640000t2 + 810000t2]
x = odmocnina z [1450000t2 - 8000 t + 25]
x = 1/2 krát (1 / odmocnina z [1450000t2 - 8000 t + 25]) krát (2900000t - 8000)
Dát derivaci rovno 0
0 = 1/2 krát (1 / odmocnina z [1450000t2 - 8000 t + 25]) krát (2900000t - 8000)
Z toho vyplývá, že
2900000t - 8000 = 0
2900000t = 8000
t = 0,0027586 hod.
t = 9,93 vteřiny
Jestli jsme neudělal chybu, tak nejmenší vzdálenost mezi letadly bude za 9,93 vteřiny.
Dosazení do rovnice za t
x = odmocnina z [(5 - v1 krát t)2 + (v2 krát t)2]
x = odmocnina z [(5 - 800 krát 0,0027586)2 + (900 krát 0,0027586)2]
x = odmocnina z [7,8 + 6,17]
x = 3,74 km
Tedy bezpečnostní vzdálenost 3,5 km byla při letu dodržena.
doplněno 06.11.20 20:14:
V okamžiku, kdy je zjištěna pozice letadla B radarem, je t = 0
V tom jednom řádku se u x nezobrazila čárka značící derivaci (kvůli něčemu to nejde, zobrazit tento znak)
Tedy napsáno jinak
derivace x = 1/2 krát (1 / odmocnina z [1450000t2 - 8000 t + 25]) krát (2900000t - 8000)
V kvadratické funkci
[(5 - v1 krát t)2 + (v2 krát t)2] = y
lze spočítat x ovou souřadnici vrcholu paraboly (doba t je znázorněna na ose x).
A lze tak zjistit bez derivace dobu t, při které je minimální vzdálenost.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.