Nejste přihlášen/a.
Asi jsem se v tom moc zamotala. Děkuji moc
3x
Zdravím. Úvodem trochu teorie: Těžnice trojúhelníka je úsečka jejímiž krajními body jsou vrchol trojúhelníka a střed protější strany. Trojúh. má tři těžnice, které se protínají v jednom bodě - těžišti. Obvyklé značení: těžnice z vrcholu A: ta , z vrcholu B: tb atd., těžiště: T. Těžiště rozděluje těžnici na dvě části v poměru 2:1. Vzdálenost vrcholu od těžiště je dvakrát větší než vzdálenost těžiště od středu příslušné strany. Nebo-li: úsečka AT= 2/3 ta , úsečka TA0= 1/3 ta , (A0 je střed strany a). Přikládám zápis postupu konstrukce a konstrukci...
1x
Přiznám s, že při bližším pohledu nechápu Vaše zadání. Minimálně máte dvě úsečky označeny stejně, totiž l:
teznice k =5cm, stranal= 6cm, teznice l=6cm
navíc není jasné, kterou těžnici by mělo písmeno l označovat.
Můžete napsat zadání znovu a poříádně?
Zdravím.
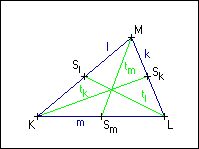
Také jsem se pozastavil nad formou zadání (strana l, těžnice l...). "Těžnici l" jsem pochopil jako těžnici z vrcholu L - obvyklé značení tl a "těžnici k" jako těžnici z vrcholu K - tk ... Takže zadání (dle mého mínění): Trojúh. KLM: l=6 cm, tk=5 cm, tl= 6cm
0x
Myslím, že řešení je tady
doplněno 23.10.20 22:17:
Myslím si, že postup je takto:
Těžnice se protínají ve 2/3 jejich délek, tedy v těžišti T
Narýsovat stranu KM
Udělat střed S strany KM
Z bodu K narýsovat kružnici n, jejíž poloměr je o velikosti 2/3 délky těžnice na stranu k
Z bodu S narýsovat kružnici m, jejíž poloměr je o velikosti 1/3 délky těžnice na stranu l
Kde se kružnice m,n protnou, tak je bod T (těžiště)
Narýsovat polopřímku MT
Délku střed S1 úsečky MT
Vzdálenost /S1T/ nanést na polopřímki MT, "za "bodem T
Tak vznikne střed strany KL
Následně narýsovat stranu KL .
---
Je to taková "krkolomná"konstrukce
doplněno 23.10.20 22:24:
oprava:
Udělat střed S1 úsečky MT
Vzdálenost /S1T/ nanést na polopřímku MT, "za"bod T
Tak vznikne střed S2 strany KL
Následně vzít do kružítka vzdálenost KS2 a narýsovat stranu KL .
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.