Funkce, graf

Možná to udělat tak, že by grafem funkce byl graf y = 1/x pro D(f) = R - {0}, přičemž pouze v bodě x = 0 by funkce byla definována konstantní funkcí, třeba y = 1.

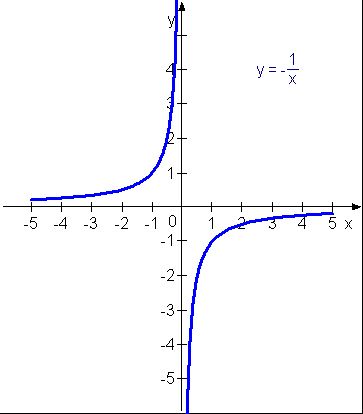
Takže výsledným "grafem" byl třeba graf y = - 1/x a k tomu ta tečka třeba v bodě [0;1] (ta není v tom druhém grafu znázorněná).

Ale toto je taková "krkolomná konstrukce".

oprava:

Takže výsledným "grafem" může být ...

Zadání má být správně se složenou závorkou, tedy takto- H(f)= R - {0}

Definiční obor je lidově napsáno - množina čísel, které lze do předpisu funkce dosadit za x.

Obor hodnot je lidově napsáno - množina čísel, které mohou vyjít jako y.

Možná se to dá tak, že

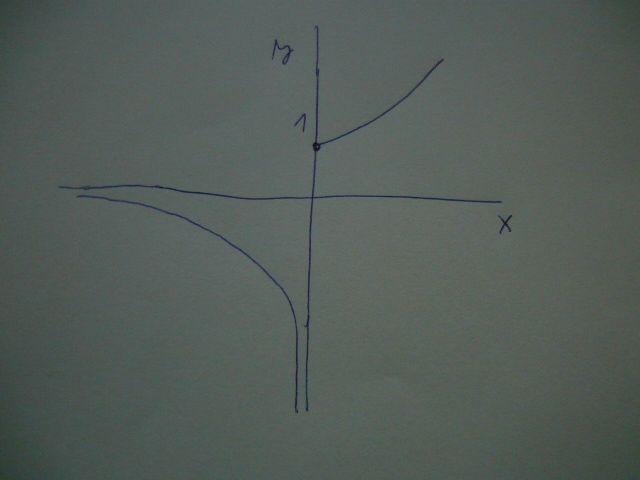
pro část definičního oboru <0; nekonečno) je předpis funkce definován jako a^x

pro část definičního oboru ( mínus nekonečno;0) je předpis funkce definován jako a/x

Tedy ve 3. kvadrantu je část grafu funkce hyperbola a v 1. kvadrantu je část grafu funkce část exponenciální funkce, přičemž a je nějaké kladné číslo

Ne, takto to nejde, protože v tom případě by nebyla "pokrytá" část osy y od 0 do 1

Asi blby, ale co treba maticova funkce...

B=f(x)*A, kde A je matice (1, -1), at uz sloupcova nebo radkova a f(x)=e^x (treba)

Pak B=(e^x, -e^x).

x nalezi R; B lezi v R krome 0.