Nejste přihlášen/a.
Mám síť tělesa (hranol, jehlan, kužel, válec), jak vypočtu maximální rozměry, aby se mi jeho síť vešla na papír?
Matně vzpomínám, že jsme něco podobného počítali a šli na to nějak přes derivace.
1x
Tahle úloha by chtěla trochu upřesnit. Miramira má pravdu v tom, že objem tělesa a obsah povrchu je vlastně úloha integrálního počtu, ovšem obecně by šlo o objemový či plošný integrál a u výše popsaných těles vystačím s elementární geometrií, integrál by tu byl kanon na mouchu. Derivování je technika, používaná na hledání extrémů, ale tady bych se ptal, extrém čeho hledám? A taky co znamená, "aby se vešla na papír"? to druhé může znamenat, že ji chci (tu síť) na papír namalovat "tak jak je", nebo že ji chci z papíru vystřihnout třeba po kouskách a různě poskládat. A ty maximální rozměry. třeba válec má minimálně dva základní rozměry - výšku a průměr základny (pokud je kruhová), a roli bude hrát ještě obsah pláště a základny, a taky jeho objem, co chcete maximalizovat?
doplněno 23.10.10 10:51:Ad válec: cs.wikipedia.org/... (nejen že válec nemusí mít základnu kruh, ale může být i kosý, tedy šikmý - ten "úhel zešikmení"je další možný parametr.
- Síť tělesa se vystřihne jako celek. Papír A4. Budou to různá tělesa o různých rozměrech, krychle, kvádr, hranol, jehlan, válec, kužel, koule prý neexistuje jako síť
- On válec nemusí mít základnu kruh? Samozřejmě to může být i elipsa, ale to pak se už asi nejmenuje válec. Jak se to pak jmenuje?
- Já si matně vzpomínám, že jsme něco podobného počítali v matematice (jestli to byli integrály nebo derivace to si už nepamatuji), ale vím, že jsme měli zadanou síť tělesa a měli jsme vypočítat rozměr tělesa. Co to bylo za těleso si už nepamatuji.
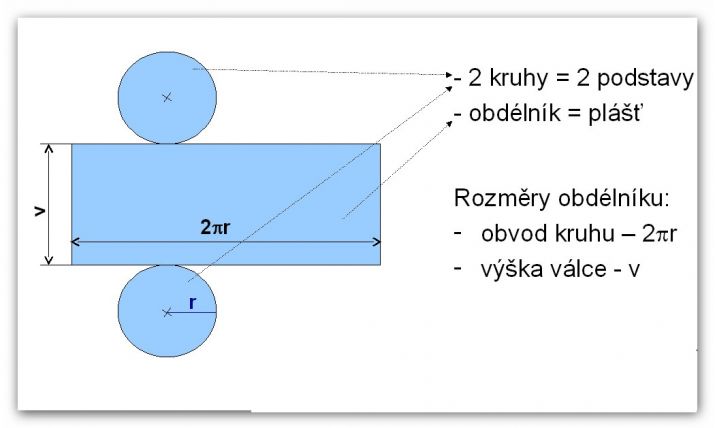
Takže zkusme se podívat na rotační válec s pláštěm jako na přiloženém obrázku, a mysleme si, že ta síť je na A4 položena tak, že základny jsou na výšku, tedy že, v termínech obrázku) 4r + v < a = 197(cm), 2Pí r < b = 210 (cm). První podmínka, aby se plášť na papír vešel, je tedy r <210/2Pí, což je méně než 210/6 = 45 (pak bude i r < 197/4 = 49,25) Pokud budeme mít válec s poloměrem základny r, pak v může být až a - 4r. Takový maximální válec bude mít objem [Pí r^2 *(a-4r)] základna krát výška) a obsah povrchu [Pí r^2 + 2Pí r * (a-4r)] (základna plus plášť). A teď záleží na tom, co chci maximalizovat, zda povrch nebo objem. Podle toho příslušný vzorec zderivuji podle r, položím rovno nule a vypočtu r. Musím se přesvědčit, zda takto vypočtené r vyhovuje nerovnosti r <210/2Pí, což bude pravda, a je to.
(Úplně správné by bylo jště ověřit mezní případy r = 0 a v = 0, u objemu je jasné, že tam maximum nebude, u povrchu by to odpovídalo zvrhlému válci, ale zřejmě ani tam to nebude.)
Kdyby ten plášť byl na šířku, počítalo by se to podobně, jen bychom zaměnili a za b a patřičně upravili definiční nerovnosti.
Já mám jen střední školu ( SPŠ Rakovník) obor strojírenství a z matematiky jsem nematuroval a jiné válce než s kruhovou podstavou jsme nebrali ![]() . Mám doma učebnici matematiky pro gymnázia, tak se zkusím podívat tam.
. Mám doma učebnici matematiky pro gymnázia, tak se zkusím podívat tam.
Hyperbolický, parabolický válec si nějak nedovedu představit. Můžete jej do wikipedie nakreslit, ať neodbočujeme příliš od tématu i když je to téma zajímavé?
Na hyperbolický či parabolický válec klidně zapomeňte, to je opravdu látka trochy vyšší úrovně, speciální případ studia kvadrik, což jsou mimo jiné hyperboloidy, paraboloidu hyperbolické paraboloidy, elipsoidy, koule a další a další. Uváděl jsem to jen pro úplnost, blíže k tématu jsou ty kosé válce a válce s jinou základnou, než je kruh, ale i to je pro nás zbytečně složité. (v podstatě by šlo o kolmé válce s hyperbolickou či parabolickou základnou, )
doplněno 23.10.10 13:27:Pardon, ujel jsem, jde o studium kvadratických ploch. Kvadriky jsou o dimenzi níže, jsou to křivky a v podstatě je lze všechny snadno vyjmenovat: elipsa (a kruh jako zvláštní případ), hyperbola a parabola. A to je všechno, nemluvě o různých degnerovaných případech jako hyperbola, která zdegenerovala na dvě zkřížené přímky. Už z tohoto srovnání je vidět, že teorie kvadratických ploch bude dost složitá.
Možná mimo "mísu", ale jen si oživit znalosti staré půl století. Mám dvě kruhové podstavy (dvě podstavy válce) a tyto po obvodu vzájemně propojím nitěmi, které jsou kolmé k podstavám. Obálka nití s podstavami tvoří válec. O tom není řeč. No a když jednu podstavu pootočím okolo osy o nějaký úhel vůči druhé podstavě, začne obálka těchto nití tvořit hyperbolický válec? Ano či Ne
No já mám strojní průmyslovku a tomuto jsme v předmětech Mechanika, Stavba a provoz strojů, Strojírenská technologie, Kontrola a měření říkali zkroucení.
Diskuze se začíná stáčet trochu jinam, NIC PROTI, jen bych poprosil ke každému názvu (paraboloid, hyperboloid, ...) obrázek. Ne každý kdo to čte studoval MatFyz ![]() a nebo si to představit jak to vypadá.
a nebo si to představit jak to vypadá.
DEKUJI za pochopení
Příklad (rotačního) paraboloibu: upload.wikimedia.org/...
další související obrázky třeba na cs.wikipedia.org/...
Rotační jednodílný hyperboloid:: cs.wikipedia.org/...
(například vysílač na Ještědu).
Dvoudílný hyperboloid: cs.wikipedia.org/...
(převzato z cs.wikipedia.org/... Jinak je to dost pestrá škála možností, třeba na commons.wikimedia.org/... je něco.
Zajímavé obrázky ![]()
Kde se s těmito "tělesy"a plochami člověk setká v praxi? Kdy je potřeba znát objem nebo povrch hyperbolidu,parabolidu?
Pokud zavzpomínám na matematiku tak jsme si říkali, že u některých funkcí je grafem hyperbola nebo parabola (ted si nejsem jistý, ale parabola je u kvadratických funkcí). Když jsme brali rovinné útvary (planimetrii) tak jsme si maximálně řekli rovnici paraboly a hyperboly a víc nic.
A to jsme byli technická škola ( SPŠ Rakovník). Do jaké hloubky se to asi bere na ekomických, zemědělských,hotelových,zdravotních školách.
Proč se to učí až na vysokých školách? V tom je ještě nějaký háček, že se to nemůže nakreslit do učebnice a napsat k tomu vzoreček.
Na ZŠ jsme se učili vzorečky zpaměti. Na střední škole jsme vzorečky nemuseli umět zpaměti (některé jo, např. goniometrické funkce, roznásobování mnohočlenů,...)To jsme si nosili do hodin tabulky a učitelka nám říkala, aby jsme se neučili stylem S= (a+c).v /2 ale abychom se je učili stylem sečteme dolní a horní základnu, vynásobíme výškou a celé to lomíme 2. Ve 3ťáku a čtvráku jsme si začali říkat jak ty vzorečky vznikli. Že to není že nějaký pán řekl že koule se bude počítat takhle, ale učitelka nám to zintegrovala. potom vyšel vzorec co je uveden v matematicko-fyzikálních tabulkách (MFChT).
Různé tu kvadratické plochy (paraboloidy, hyberboloidy, atd) se uplatnují třeba v architektuře, Zmínil jsem ten Ještěd, různé skořepinové konstrukce, zajímavé fotky jsou třeba na mat.fsv.cvut.cz/...
doplněno 23.10.10 16:47:Nebo třeba "parabola"od satelitu.
doplněno 23.10.10 16:48:A ještě mi napadá hladina vody v rotující nádobě. Tak Wichterle vyrobil první kontaktní čočky.
No alespoň jsem si ujasnil, že ta plocha tvořená z "nití" (viz výše) je v kolmém řezu hyperbola.
A pro Michala. Nevím který je ročník, ale nás za "totality" před padesáti lety se toto na strojní průmyslovce učilo. Zdá se, že tenkrát se učily i užitečné věci.
A při maturitě mohly být na lavici jak slovníky, tak tabulky. S cílem nemusíš vše znát z paměti, důležité je vědět kde se to najde.
Za to dnes při zkušebních maturitách na lavici nic a student se nesmí jít ani vych... aby náhodou někde něco neopsal.
doplněno 24.10.10 00:05:A jen tak mimochodem. Objem koule jako integrál suma "válců" a výšce delta blížící se k nule a o průměru od nula po 2R kružnice jsme integrovali sami.
Asi na to bylo víc hodin matematiky. Dneska je víc předmětů navíc např. počítačová grafika, programování strojů a aby nebyli studenti ve škole do večera, muselo se někde ubrat. Matematiky jsme měli asi 3 hodiny týdně ve vyšší ročníkách (v prváku asi 5) a látky bylo stejně jako v prváku jak říkala pani učitelka, proto pořád jela dál bez ohledu na to, že mnozí ještě látku nepochopili a měli z ní čtyřky.
U maturity lze mít tabulky, kalkulačku, ale musí být předem zkontrolovány.
To snad bude případ od případu. Záleží zda to bude třeba válec a budou to 3 kusy, nebo čtyřboký jehlan z jednoho kusu.
Derivace se spíš použijí naopak, abych zjistil rozměry krabice s největším objemem z jedné dané tabule.
Tak ono je to různé. Diferenciální počet nabízí celkem univerzální nástroj k řešení extremálních úloh, jiné postupy je třeba volit podle konkrétní úlohy. Často lze použít nerovnost mezi aritmetickým a geometrickým průměrem, která říká: označíme-li aritmetický průměr n kladných čísel (tedy jejich součet dělený n) písmenem s a jejich geometrický průměr (tedy n-tou odmocninu z jejich součinu) písmenem g, pak g je vždy menší nebo rovno s a rovnost nastává tehdy a jen tehdy, jsou-li všechna ta čísla sobě rovna. Použití mohu ilustrovat na jednoduché izoperimetrické úloze, zvané Didonina úloha:
Podle pověsti dcera tyrského krále Dido (umírá okolo roku 890 př.n.l) utekla od otce. Na severním pobřeží Afriky pak chtěla zakoupit území za cennosti, které si s sebou přivezla. Numidský král Hiarba kupodivu souhlasil s prodejem pozemku na mořském pobřeží, ale "ne větší, než jakou lze ohraničit volskou kůží". Dido však tento lstivý kousek krále Hiarba vrátila i s úroky. Rozřezala volskou kůži na tenké proužky, které pak navázala a dostala tak provázek o délce l, kterým ohraničila pozemek s maximální výměrou. Dido se pak stala první legendární královnou právě založeného Kartága. Otázkou je, jaký obrazec Dido ohraničila, aby měl maximální možnou výměru?
Matematicky to znamená, že hledáme rovinný obrazec, který má při daném obvodu (perimetru) největší obsah. Kompletní řešení vede na kruh a kružnici, ale to je trochu složitější záležitost. Dodáme-li předpoklad, že hledáme obdélník s největším obsahem (třeba proto, že chceme, aby Kartágo mělo pravoúhlé hradby) úloha se rázem zjednoduší.
Hledáme obdélník o stranách a, b s daným obvodem o = 2(a+b) tak aby obsah V = ab byl co největší. Zde vidíme, že aritmetický průměr čísel a b je s = o/4 a že V=g^2 Z toho plyne, že V je nanejvýš (o/4)^2 a rovnost nastane, když a = b, tedy pro čtverec.
doplněno 27.10.10 09:07:Ještě bych doplnil, jak lze tuto metodu použít na problém válce s maximálním objemem. Jak snad patrno, metoda spočívá v tom, že hledáme-li maximální součin čísel, jejichž součet je konstantní, položíme mezi tato čísla rovnost (tedy pokud to jde, samozřejmě).
V našem případě chceme maximalizovat výraz
[Pí r^2 *(a-4r)]
což je součin tří čísel: r, ještě jednou r a (a-4r).(a samozřejmě konstanty 2Pi, ta ale nehraje roli). Na první pohled se zdá, že zde metodu nelze použít, protože součet není konstantní. Pomůžeme si trikem: budeme hledat maximum čtyřnásobku a trochu si to upravíme:
4*[Pí r^2 *(a-4r)] = [Pí (2r)^2 *(a-4r)]
a vidíme, že 2r + 2r + (a-4r) = a už konstantní je a maximum nastává pro 2r = (a-4r), tedy pro r= a/6.
(Ten druhý případ vyřešíme podobně, jen budeme muset vytknout Pí*r, pro začátek.)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.