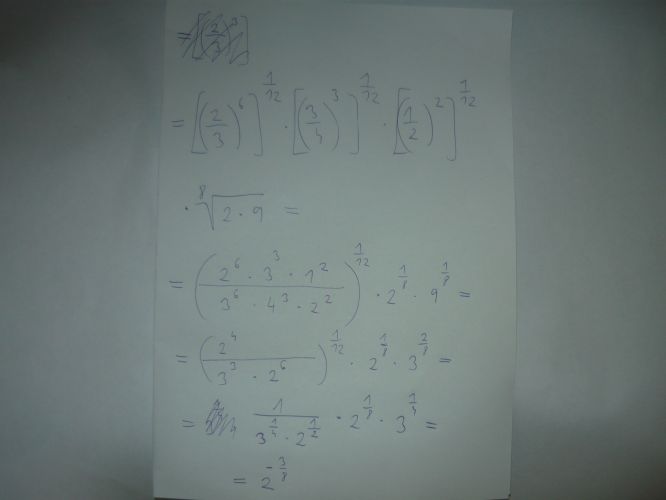Nejste přihlášen/a.
A také, jak se počítají takovéto typy úloh (např. ta 5. úloha, vůbec nechápu, jak tam mám vymyslet rovnici)? ( su.rubesz.cz/... vím, že to jsou sl. úlohy o pohybu, ale od toho 4. příkladu, mi už pohybovky nepřipomínají...Jak to počítáte vy? Děkuji
doplněno 23.08.20 17:02:
doplněno 23.08.20 17:06:
Omlouvám se, nevložil jsem tam tento příklad, a ten odkaz už by měl fungovat![]()
Třeba v 5. příkladě pohyb nehraje žádnou roli. Důležitý je stejný čas a stejná rychlost. Pochopitelně při stejné rychlosti a stejném čase je uběhnutá stejná dráha. Ovšem zadání děs. Teprve z řešení jsem pochopil, že běžec uprostřed předběhl na druhou stranu přes trávník přes středovou čáru.
Zdravím. V předposlední řádce by se mi víc než "dvě na jednu polovinu" líbilo "dvě na jednu šestinu" . (Pokud je v čitateli místo 24 číslo 1).
1x
Př. 4
Rychlost plavání ... vp
Rychlost běhu ... vb
Obecně rovnice pro rychlost je v = s / t
t = s / v
Doba plavání ... tp
Doba běhu ... tb
tp = 2 / vp
tb = 10 / vb
tp + tb = 3
2 / vp + 10 / vb = 3
Druhá rovnice je takto (zaměněny rychlosti)
2 / vb + 10 / vp = 7
Vznikla soustava dvou rovnic o dvou neznámých
Místo 1 / vp dát x
Místo 1 / vb dát y
Úpravou vznikne
2 x + 10 y = 3
2y + 10 x = 7
-10x - 50y = - 15
10x + 2y = 7
- 48y = - 8
y = 1/6
x = 8 / 12
vp = 1,5
vb = 6
Jaké vymejšlení. Komu není shůry dáno. Snad by jsi měl umět vypočítat rychlost když znáš čas a dráhu. Máme dvě neznáme rychlosti, ovšem známe celkovou dráhu a čas.
Sečteme dva úseky 2 a 10 km s neznámou rychlosti v1 a v2 s celkovým časem 3 hodiny, pak rychlosti otočíme a sečteme dva úseky 2 a 10 km s rychlostí v2 a v1 s celkovým časem 7 hodin.
Máme dvě rovnice o dvou neznámých a výpočteme neznámou v1 a v2
1x
Př. 6
Protože Adam šel dvojnásobnou dobu, tak lávka ke které šel Adam byla dvojnásobně vzdálená než druhá lávka.
Vzdálenost od přívozu k bližší lávce označím s
Celkem vzdálenost mezi lávkami je 3s
Když Adam přešel přes lávku, tak Boris byl od něj vzdálen 2s.
Tedy na druhé straně řeky se potkali ve vzdálenosti s od přívozu (na straně ke vzdálenější lávce)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.