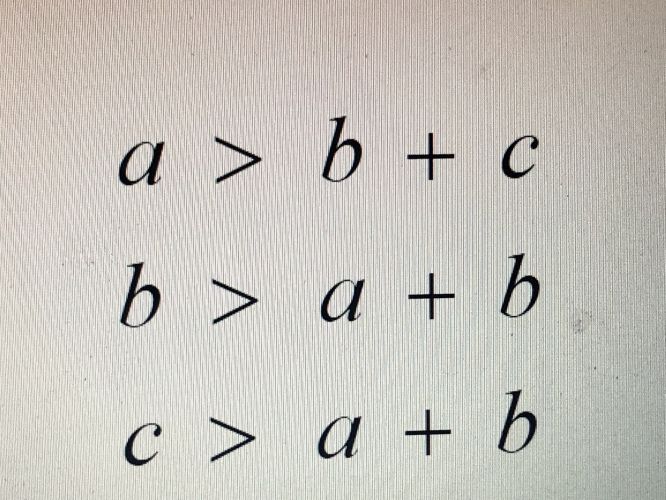Nejste přihlášen/a.
2x
Řekl bych, že součet dvou stran v trojúhelníku musí být logicky větší, než strana třetí.
Chybu vidím v matematickém vyjádření:
a < b + c
b < a + c
c < a + b
1x
Zdravím a doporučuji navrhnout na vyznamenání toho, komu se podařím sestrojit trojúhelník, v němž součet dvou stran je menší než strana třetí...
Trojúhelník. Definice.
Správná je. Součet dvou stran je větší než strana třetí
Špatné je. Součet dvou stran je menší než strana třetí.
Zrovna tak je špatně. Součet dvou stran je stejný jako strana třetí.
@priklad1: Pokud je součet dvou stran "trojúhelníka" stejný jako třetí strana, nejde o trojúhelník nebo přímku, ale o úsečku. Proto opakuji dotaz: PROČ JSI PSAL TOTO: "Ani hop to nemá správně. Má tam mít <="? ![]()
Protože je li součet dvou stran menší než třetí strana, tak to není trojúhelník
Zrovna tak je li součet stejný jako třetí strana, tak to není trojúhelník.
Co je na tom nepochopitelného.
Já už nemám chuť se vracet k napsanému textu. Vím na co jsem reagoval
Sklidem připouštím, že jsem se mohl překouknout.
Ale taky vím na 100%, že se již několikrát text od pisatele v rámci povolených pěti minut změnil a to dokonce diametrálně.
0x
Obecná podoba trojúhelníkové neroivnosti pro tři čísla a,b c je skutečně
a+b≥c, slovy součet dvou čísela,b je větší nebo roven (jinak, nemůže být menší) tředímu. Trojúhelník toilistruje,ale obecně je to prostě nerovnosts mnohým použitím, napříklat patří kaxiomům metrických prostorů (kdy čísla a,b,c jsou vzdálenosti a = ρ(B,C), b = ρ(A,C), c = ρ(B,A)). Ovšem pokut ji aplikujenme na geometrický trojúhelník a nebereme doúvahy "zvrhlé" trojúhelníky, které zdegeneruvalu v jednorozměrný útvar, pak pak rovnost nenastává. Takže tohle bych panu učiteli snad ani nevyčítal, ovšem "obrácený zápis" nerovnosti pomocí nerovnítek už je přepis, který by u žáků pan učitel dalžákovi kuli.Ale lidé jsou chybující a přepis se stát může; nebylo by lépe obrátit se přímo na pana učitele? Jistě by se opravil.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.