Zdravím, jak určím součet nekonečné řady? Zkusil jsem určit vzorec an = (n+6)/(n(n+1)(n+2)) jestli to tak je a k něčemu je.
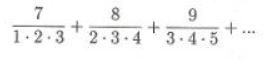
3x
Někde jsem četl příklad.Jak sečíst za 1 minutu všechny čísla o 1 do 100?
Způsob sčítání je závislý na logickém myšlení.
Sečteme první a poslední číslici v řadě.- činí to 1 + 100 = 101
pak druhé a předposlední - 2 + 99 = 101
Takto postupujeme celou řadou a poslední co počítáme že všech dvojic je 50-tedy 50 x 101 = 5050
Napsat to mi trvalo 1 minutu.
JABRAKA
2x
Musím se přiznat, že už stárnu a tenhle součet mi dělá problémy. Stejně si myslím, že by to mělo nějak relativně snadno jít z toho rozkladu (n+6)/(n(n+1)(n+2)) = -5/(n+1) + 2/(n+2) + 3/n, ale nějak na to nemohu přijít. Mohl bych ještě přemýšlet,ale dopustím se lehkého podvůdku a zeptám se Wolframa, který mi napoví, že částečný součet té řady od 1 do m je roven
((m*(2m+5)/((m+1)*(m+2)).
Limita tohoto výrazu pro m jdoucí do nekonečna je rovna 2, no a i když jsem tento částečný součet vlastními silami nevymyslel, natolik si fandím, že bych ho uměl dokázart matematickou indukcí (ale dělat to nebudu,ať má co dělat taky Bruno.
Díky za snahu, já jsem s tím taky nehnul. Taky jsem to zkusil přes parciální zlomky. Pak jsem vždycky určil pomocí částečných součtů vzorec pro sn = .. ,ale zde se mi nic nerušilo a ani jsem žádnou souvislost nenašel. Trápit se s tím nebudu..zbylých 5 podobných příkladů jsem spočítal, takže i tak dobrý.
0x
Nevím, jestli je možné to vypočítat teoreticky jako limitu, kde n se blíží nekonečnu.
Je možné to spočítat s určitou přesností, např. na desetitisícinu.
(n+6)/(n(n+1)(n+2)) je menší nebo rovno 0,0001
Odhadem n = 100
106 děleno ( 100 krát 101 krát 102) = 0,000103
Samozřejmě na kalkulačce je pohodlnější to spočítat s přesností na setinu
Pro n = 10
0x
Limita výrazu (n+6)/(n(n+1)(n+2)) pro n jdoucí do nekonečna je zcela evidentně nulová (a tento váraz klesá k nule rychlostí 1/n²), Problém, o který tu jde, je sečíst příslušnou nekonečnou řadu. (Samozřejmě souvislost tu je. Nulová limita n-tého členu je nutnou podmínkou konvergence, a ta výše zmíněná rychlost zaručuje již konvergenci (srovnávací kriterium).)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.