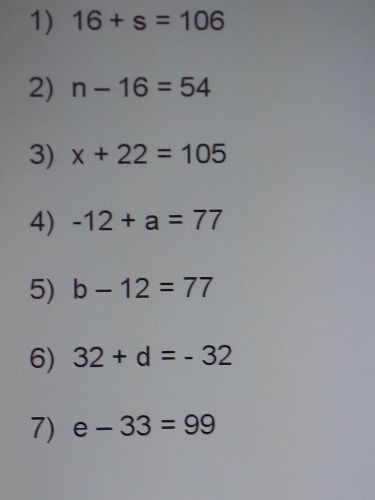potřeboval bych poradit, jak se počítá ekvivalentní úprava rovnic. Zkoušel jsem to počítat, ale prý mi to vůbec nevychází.
Tak každou radu budu moc rád.
1x
Zdravím.
Možná by bylo vhodnější:"...jak se provádí ekvivalentní úprava rovnic..." Ekvivalentní úpravy jsou takové úpravy, při kterých se stejným způsobem mění levá i pravá strana rovnice. Kořen rovnice se nemění... Ekvivalentní úpravy:
- k oběma stranám rovnice přičíst stejné číslo (výraz)
- od obou stran rovnice odečíst stejné číslo (výraz)
- obě strany rovnice násobit stejným číslem (výrazem) různým od nuly
- obě strany rovnice vydělit stejným číslem (výrazem) různým od nuly
- zaměnit levou a pravou stranu rovnice
Cílem užití ekvivalentních úprav je zjistit kořen rovnice. Takže úprava u 1) je -16 , u 2) je to +16 , u 3) pak -22 atd.
Nejčastější hrubou chybou začínajících je, že provedou úpravu jen na jedné straně...
Zdravím.
Ověření správnosti výpočtu kořene rovnice se provádí zkouškou tak, že se do původního znění rovnice (tedy do její "první řádky") dosadí za neznámou (za ono písmeno) vypočtený kořen. Zvlášť se vypočte levá (L) a zvlášť pravá (P) strana rovnice. Oba výsledky se porovnají. Při správnosti výpočtu musí vyjít L=P . Vzhledem k jednoduchosti uvedených rovnic je zkouška velice snadnou záležitostí, což ovšem u všech rovnic tak nebývá. Někdy je zkouška obtížnější než řešení rovnice...
0x
Když přesouneme tzv. člen rovnice z jedné strany rovnice na druhou stranu rovnice, tak se změní znaménko před tímto členem
Např.
e - 33 = 99
Před členem 33 je znaménko mínus a po přesunutí na pravou stranu rovnice bude znaménko opačné, tedy plus
e = 99 + 33
Před "tisíci" lety říkával pracovník KPÚ (krajský pedagogický ústav) ČB Alois Terš v souvislosti s řešením rovnic: Na druhou stranu převádíme babičku přes ulici, při řešení rovnic přičítáme, odčítáme atd. ...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.