Zdravím, mám 3 příklady, tentokrát s goniometrickými funkcemi. Zkusil jsem vybrat podle mě ten z lehčích.
a) v celém intervalu
b) v intervalu <0,2π>
Moje řešení:
q = sin2x , |q| <1
Podle grafu: x ≠π/ 2 + kπ v celém intervalu , v intervalu <0,2π> x ≠ π/ 2 a 3π/2
Dostal jsem rovnici 1 + (sin2x/cos2x) =2tgx
po úpravě: cotgx = +- 1
pro +1 mi vyšlo x` = π/ 4 a pro -1 mi vyšlo x` = 3π/ 4
Nyní jsem určil x1, x2, x3 a x4 podle znamének v kvadrantech či jak.
x1 =π/ 4 + kπ x2 = 3π/ 4 + kπ x3 = 7π/ 4 + kπ x4 = 5π/ 4 + kπ (v celém intervalu, ale nevím, zda je to dobře..)
Dotazy:
1) Určím tu podmínku sin2x >-1 a sin2x <1 i jinak než pomocí grafu?
2) Jak teď sladit výsledek s podmínkou?
2x
Přčiznám se. že á bych volil jiný postup řešení, ale ten váš je súpávný a výsledek je dobře. Snad bych jen upozornil, že nerovnost sin ² x >-1 je automatická. Vám půjde, konec konců, spíš o nerovnosti -1 < sin x < 1, což vzhledem k vlastnostem sinu je vlastně podmínka sin x různé od plus mínus jedné.
A co se týče otázky, jak sladit výsledek s podmínkou, té tak trochu nerozumím. Oč vám jde? Prostě podmínka (\q\<1 je podmínkou nutnou a postačující pro konvergenci té geometrické řady, a součet, který vám vyšel, při nesplnění konkrétní podoby nedává smysl (mšl byste ve jmenovateli nulu), takže vo co gou? Jistě, v některých případech se může stát, že ze vzorce pro součet geometrické řady dá výraz, který formálně dává smysl i pří nesplnění podmínky konvergence, pak to ovšem není součet a můžeme se ptát, co si o tom myslet, ale tady nic takového nehrozí.
doplněno 20.04.20 19:15:
V tom textu je chyba, ktero nechaápu a kterou se mi nepodařilo opravit, zkusím to v doplnění.
Na konci prvníhoodstavce po "spíš o nerovnosti -1" mělo bát: "spíš o nerovnosti -1 < sin x < 1,
což vzhledem k vlastnostem sinu je podmínka sin x ≠±1.
A zase se to nepovidlo opravit zcela, něso tam hapruje, zkusím místo symbolů slova:
V tom textu je chyba, ktero nechaápu a kterou se mi nepodařilo opravit, zkusím to v doplnění.
Na konci prvníhoodstavce po "spíš o nerovnosti -1" mělo bát: "spíš o nerovnosti -1¨menší než sin x menší než 1,
což vzhledem k vlastnostem sinu je podmínka sin x ≠±1.
Ted jsem si všiml, že tam mám chybu... Já ten součet té řady dělal až od toho druhého členu, jedničku jsem pak přičetl.
s = sin2x / (1-sin2x) = sin2x / cos2x
Tedy dostanu 1 + (sin2x / cos2x) = 2 tgx
A tady mám chybu. Platí, že tg x = sinx / cosx , ale já tam nevím, proč mám na druhou 2*( sin2x / cos2x)
A dál se dostanu k tomu výsledku, který jsem napsal v zadání.
Tak jsem se dopočítal.
1) Kdybych nedal omylem u toho 2tg x , že se rovná 2* (sin2x/cos2x) , ale správně jenom na prvou, tak mi vyšlo nakonec tvar 1 = sin2x ( nyní už jsem si nevěděl rady, možná vzorec pro dvojnásobný úhel, jestli by nějak pomohl, nevím)
2) Každopádně jsem to udělal celé jinak, a to : 1 + tg2x = 2tgx. Pak mi vyšlo π/4 a 5π /4 v tom omezeném intervalu viz zadání.
Jdu ještě chvíli zápasit s dalšími dvěma.
Já jsem v zadání uvedl ten tvar rovnice a pak už rovnou výsledek. Tady u toho vzorce jsem právě dal druhou mocninu, nevím proč.
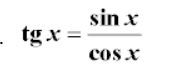
Takže zřejmě ta vaše chyba zůstala skryta ve výpočtech, které jste nám neukázal. A protože výsledek jsem očekával toho typu, že tam bude nějaká tangenta či kotangenta něčemu rovná jako řešení kvadratická rovnice, tak jsem chybu při zběžné kontrole "popaměti" neodhalil ani podle výsledku.
No ale už je to vyřešeno, snad.
2x
Jak jsem slíbil, vracím se k tomu. Ono to vaše řešení je celkem stručné, nicméně v podstatě O.K. , ale já to taky částečně sledoval zpaměti, takže se to teď pokusím probrat podrovněji.
Nejprve kvocient a podmínka konvergence. Jde skutečně o geomentreickou řadu s kvocientem q = sin² x a podmínka konvergence je |q| <1, tedy sin² x <1. Tady jste dospěl k tomu,že podmínka je splněna pro x≠½π+kπ, k celé. Ta podmínka je určena správně, jen díky stručnosti vaší odpovědi není úplně jasné, jak jste konkrétně k ní došel. Něco naznačije jeden z vašich dotazů, totiž dotaz: 1) Určím tu podmínku sin2x >-1 a sin2x <1 i jinak než pomocí grafu?
K tomu jsem již něco napsal, konkrétně jsem upozornil na to, že podmínka sin2x >-1 vás vlastně nezajímá, ta je díky nezápornosti druhé mocniny splněna automaticky. To jste si snad už promyslel, dodám poznámku k vlastnímu dotazu: nevím přesně, co myslíte tím, že ji určujete z grafu a zda to jde jinak. Pravděpodobně použávíte toho, co víte o grafu, tedy nulové body, kde sin roste a kde klesá atd. To jsou ale základní vlastnosti sinu, někdy se berou jako definice sinu (a cosinu). Tady bych se tím netrápil, nicméně pro vaši informaci mohu říci,že nějakouteorii goniometrickych funkcí lze budovat třeba přes Taylorovy rozvoje, nebo dokonce pomocí diferenciálních rovnic, a vazbu ke geometrické definici sinu (jako poměr protilehlé odvěsny k přeponě) lze do toho zabudovat "heuristicky". To jsou ale hlubší až filozofické otázky a podrobnosti bz vzdaly na delší stať, klidně se múžete opírat ve školské matematice o ty základní vlastnosti. Jen ještě jeden pohled: z těch základních vlastností víme, že sin a cos jsou v absolutní hodnotě nejvýše jedna a tak podmínka konvergence vlastně znamená, vyloučit ta x, pro která je sinus plus nebo mínus jedna, což,díky goniometrické jednotce ,sin²x + cos²x = 1, je totéž, jako vyloučit cos x = 0.
No, tohle už je dost dlouhý text,takže to zatím ukončím a pokračovat budu třeba v doplnění příspěvku či v další odpovědi.
doplněno 21.04.20 18:19:
Dobrá , to bychom měli k tomuto.Teď se hodlám věnovat vlastnímu řešení.
Vaše vyjádření součtu řady: v podobě 1 + (sin2x/cos2x) je správné, o když mne malinko překvapilo, jak jste se k němu dopracoval. Já bych byl použil součet ve tvaru 1/(1-sin²x) , a možná bych ho ještě upravil do podoby 1/cos²x. Nicméně tojste vysvětlil tím, že jste nejprve udělal součet oddruhého členu a k tomu přičetl jedničku; odtud se k vašemu vzorci je možné se dopracovat celkem přirozeně.. Samozřejmě ono to musí dát totéž (tedy pokud jeden či druhý řešitel neudělá chybu) a taky lze jednu podobu na druhou převést. V každém případě oba tyto vzorce mají ve jmenovateli kosínus a tedy jsou definovány pro nenulový kosínus, což, jak jsme si řekli, je zároveň jedna z podob podmínky konverkence. Takže není žádný problém ve slaďování výsledku a podmínky, v našem případě je to totéž; tolik k Vaší druhé otázce. (2) Jak teď sladit výsledek s podmínkou?)Lč k řešení rovnice.
Když se dívám na to, co jste napsal, já tam nikde žádnou 2*tg²x nevidím, máte tam zcela ve shotě se správným výsledkem vztah 1 + (sin2x/cos2x) =2tgx čili 1 + tg²x =2tgx, což vede na kvadratickou rovnici pro tongentu, kterou lze upravit do tvaru (1-tg x)²= 0 s řešením tg x = 1. Vy jste ovšem uvedl jako řešení cotg x = ±1 a tam je chyba, ne v somotné rovnici. CHyba je dvojí: jednak jste psal cotg mistpo tg, což by ale ale , čirou náhodou nevadilo, protože tangenta ea cotangenta jsou vavzájem reciproké a když je jedna znich rovna jedničce, ta druhá taky. (ovšem jistým varováním by měl být fakt, že zatím ve všech výpočtech byl ve jmonovateli kosinus a teď se tam najednou dostal sinus-) Podstatná chyba ovšem byla v tom mínus, k tomu prostě není důvod. Nicméně obě tyto chyby jsem přehlédl díky tomu , že jsem to kontroloval zpaměti. VY jste to ale stejně opravil ve své poslední poznámce, alespoň výsledek která uvádíte, tedy jednak x = ¼π a jednak x=¼π +π , je správný. Takže tím bychom tp mohli uzavřít,prostě vše jste vyřešil a doufám, že i všemu porozumněl. leč mohu vás potěšit: ta druhá podoba rovnice, totiž sin 2π = 1, je také správně a kduž se na to podíváte pořádně, jiistě ji i vyřešíte: víte přeci, pro jaké hodnoty argumentu nabývá sinus kodnoty 1, ne? Jen su uvědomte, že když x probíhá od nuly do 2π, tak 2x probíhá od nuly do 4π.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.