1x
x²+y²=4r²
V=((Pí x²)/4) y
x průmer válce
y výška válce
Zderivujeme a položíme rovno 0 pro jaké x
Tak
To je blbě. Jedná se o objem. Zadání je obsah pláště
Takže
P = Pí x y
Další postup stejný
Předpokládám, že podstavy se do pláště nepočítají
Na rozdíl od tazatele já vašemu návrhu ttak moc nerozumím. Podle čeho chcete derivovat? Jaktam zakomponujete vytah x²+y²=4r²? Neříkám, že to podle vás nejde, nebo že to máte špatně, jn mi to nepřijde úplně jasné. Ale pokud to tazatel pochopil, je to O.K.
To byl jenom nástin výpočtu objemu válce v závislosti na proměnné x. Ostatní je na tazateli z těch dvou základních rovnic vyjádřit objem V v závislosti na proměnné x a následně zderivovat.
Vlastně to měl být výpočet povrchu.
Jsou tady jiní, kteří to za tazatele celé spočítájí
1x
a)
Plocha pláště válce je
S = pí krát d krát v
d ... průměr válce
r ... poloměr válce
v ... výška válce
(2R)2 = d2 + v2
v2 = (2R)2 - d2
v = odmocnina z [(2R)2 - d2]
dosazení do vzorce plochy
S = pí krát d krát odmocnina z [(2R)2 - d2]
zderivovat
S = pí krát odmocnina z [(2R)2 - d2] + pí krát d krát 1)2 [(2R)2 - d2]- 1/2 krát (-2d)
0 = pí krát odmocnina z [(2R)2 - d2] + pí krát d krát 1)2 [(2R)2 - d2]- 1/2 krát (-2d)
po úpravě (vynásobením tou odmocninou) je
0 = pí krát R2 - 2 krát pí krát d2
2 krát pí krát d2 = pí krát R2
d = R/ odmocnina ze 2
doplněno 10.04.20 13:23:
Možná to mám chybně. Ten obrázek není úplně nejvhodnější, ale nechtělo se mně hledat jinej.
Měl by být jeden lokální extrém, který je současně i globální extrém
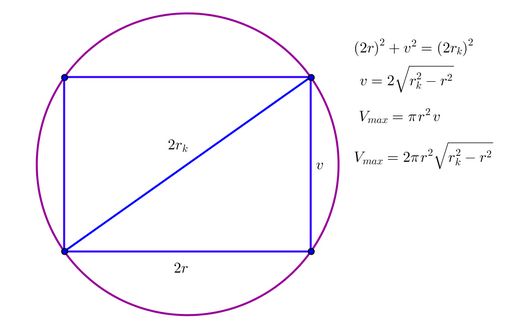
On je ten zápis trochu nepřehledné a není jednoduché se v něm orientovat, ale řekl bych,že je to dobře. Alespoň tedy sestavenírovnic a idea řešení je dobře (derivujeme yřejmě podle d) a výsledek také odpovídá. Snad jen bych dodal,žekrom tohojednoho likálního a globálního maxima to má ještě dvě lokální minima, totiž d = 0 a d = 2R, čemuž odpovídáv = 0. Tomu ovšem odpovídá !zvrhlí válec" , který degenerooval v prvním případě v kruh a ve druhém případěv úsečku, nicméně zda toto !řešení! přijmeme, záleží na tom, na jaké množině vlastně ty extrémy hledáíme; dedostatkvymezení problému v tomto směru je vlastyně trochu slabina postupu.)
1x
b)
Podstava toho trojúhelníka je a, délka ramena je b
Rotací kolem osy toho ramena vznikne tvar kuželu o velikosti poloměru a/2
doplněno 10.04.20 14:13:
Výška toho kužele je (dle pythagorovi věty)
odmocnina z [b2 - (a/2)2]
o ... obvod kuželu
o = 2 b + a
b = 1/2 (o - a)
r = a/2
Vzorec pro objem kuželu je
V = 1/3 krát pí krát r2 krát odmocnina z [b2 - r2]
dosadit za b
V = 1/3 krát pí krát r2 krát odmocnina z [(1/2 ( o - 2r))2 - r2]
zderivovat,derivaci dát rovno 0
---
V = 2/3 krát pí krát r krát odmocnina z [(1/2 ( o - 2r))2 - r2] +
+ 1/3 krát pí krát r2 krát 1/2 [(1/2 ( o - 2r))2 - r2]-1/2 krát (-( o - 2r) - 2r)
----
0 = 2/3 krát pí krát r krát odmocnina z [(1/2 ( o - 2r))2 - r2] +
+ 1/3 krát pí krát r2 krát 1/2 [(1/2 ( o - 2r))2 - r2]-1/2 krát (-( o - 2r) - 2r)
-------
0 = 4 krát odmocnina z [(1/2 ( o - 2r))2 - r2] + r krát [(1/2 ( o - 2r))2 - r2]-1/2 krát (-( o - 2r) - 2r)
0 = 4 krát [(1/2 ( o - 2r))2 - r2] + r krát (-( o - 2r) - 2r)
0 = 4 krát [(1/2 ( o - 2r))2 - r2] - or
0 = ( o - 2r)2 - 4r2 - or
0 = o2 - 4or +4r2 - 4r2 - or
0 = o2 - 5or
0 = o - 5r
r = 1/5 o
a/2 = 1/5 krát (2 b + a)
a = 2/5 krát (2 b + a)
a = 4/5 b + 2/5a
3/5a = 4/5 b
a = 4/3 b
0x
K příkladu a:
Rozvedu a zkusím zjednodušit postum podle @priklad1:
Vazební podmínka je zde tato:
x²+y²=4r²
což je, při označení, které použil priklad1 a které níže shrnuji, Pythagoyova věta
plus ještě
x≥0 y≥0
(neboť délky jaksi nmohou být záporné).
Mám maximalizovat obsak pláště, což je obtélník, jehož jedna strava , označená y, je rovna výšce , ta duhá, tedy x, je průměr válce, tedy máme minimalizovat výraz
P(x,y) = πxy
při daných vazebních podmínkách.
Postup, který měl priklad1 na mysli, je nyní tento: vypočteme y jako funkci x, po dosazení dostaneme povrch v podobě
P(x, y(x)) = f(x) = πx(4r²-x²)½
a následně standardním zůsobem (výpočet derivace atd.) počítáme maximum této funkce na intervalu <0,2r>.To je samozřejmě správné, je možné také vyjádřit x jako funkci y, ale má to jednu nevýhodu, musíte při derivování počítat s derivacemi odmocnin. To jistě umíte, ale lze to zjednodušit.
V zadání není "najděte maximální povrch" , ale "najděte válec s maximálním povrchem". No a je-li maximální (kladný) výraz f(x), je maximální i jeho kvadrát f²(x) a zůstane maximálním, i když hovydělíme či vynásobíme libovolnou kladnou konstandou, takže stačí maxi malizovat funkci g:
g(x) = x²(4r²-x²), která se derivuje mnohemjednodušejí. To si ale opravdu již vovolím přenechat tazatreli.
doplněno 13.04.20 17:58:
A na závěr ještě poradím, jak se obejít úplně bez derivování. Připomenu nějaké definice: jsou-li A,B dvě kladná čísla, pak symbolem s označím jejich aritmetický půměr
s = ½(A+B)
a symbolem g jejich geometrický průměr
g = (AB)½
No a pro tuto veličiny platí známá nerovnost AG pro aritmetický a geometrický průměr:
Pro všechna kladná A,B platí s≥g, a rovnost nastane tehdy a jen tehdy, když A = B.
My máme maximalizovat funkci P(x,y) = πxy při dané vazební podmínce x²+y²=4r². Položíme-li nyní A = x² a B = y² a spočteme oba průměry, dostaneme s = ½(x²+y²) = 2r², g = xy a z nerovnosti AG plune
xy≤2r² a rocnost nastane pro x = y, což dává právě maximální hodnotu. No a po dosazení do vazební podmínky zjeišťujeme, že válec má maximální povrch pro? (Na okraj, tímto postupem zjišťujeme ihned i velikost toho maximalizovaného povrchu.)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.