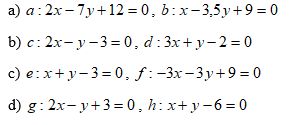1x
Ty přímky jsou zadány tzv. obecnými rovnicemi.
Vzorec obecné rovnice přímky je
ax + by + c = 0
a,b jsou souřadnice tzv, normálového vektoru, tedy vektoru, kolmého na danou přímku
př a)
normálový vektor přímky a je n a = (2 ; -7)
normálový vektor přímky b je n b = (1 ; -3,5)
Porovnáním těchto vektorů zjistíme, zda jsou dané přímky rovnoběžné (popř. splývající), různoběžné nebo navájem kolmé.
Jelikož n b je násobkem n a (dvojnásobkem) tak dané přímky jsou buď rovnoběžné nebo splývající.
Jestli jsou nebo nejsou splývající, to zjistíme vynásobením třetího čísla v rovnici.
x -3,5y + 9 = 0
9 krát 2 je 18
V první rovnici je třetí číslo 12.
Tedy přímky jsou rovnoběžné.
doplněno 04.04.20 14:33:
1x
př b)
normálový vektor přímky c je n c = (2 ; -1)
normálový vektor přímky d je n d = (3 ; 1)
Jelikož n d není násobkem n c tak dané přímky jsou buď rúznoběžné nebo kolmé.
Jestli jsou kolmé, to zjistíme skalárním součinem. Když je výsledek skalárního součinu 0 tak jsou kolmé.
Vzoreček pro skalární součin je tady
2 krát 3 + (-1) krát 1 = 5
Výsledek není 0, takže dané přímky jsou různoběžné a nejsou navzájem kolmé.
1x
normálový vektor přímky e je n e = (1 ; 1)
normálový vektor přímky f je n f = (-3 ; -3)
Jelikož n f je násobkem n e tak dané přímky jsou buď rovnověžné nebo splývající
Jelikož 9 je (-3) násobkem -3 , tak přímky jsou splývající
---------------------------------------------------------------------------------
normálový vektor přímky g je n g = (2 ; -1)
normálový vektor přímky h je n h = (1 ; 1)
Jelikož n g není násobkem n h a skalární součin je 1 tak přímky jsou různoběžné a ne navzájem kolmé
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.