Nejste přihlášen/a.
0x
Je potřeba tu zadanou rovnici upravit
4 xna2 + y na2 - 8x + 2y + 1 = 0
4 xna2 - 8x + y na2 + 2y + 1 = 0
4(xna2 - 2x) + (y na2 + 2y) + 1 = 0
4 (x - 1)na2 + (y + 1)na2 -1 -1 + 1 = 0
4 (x - 1)na2 + (y + 1)na2 = 1
na pravé straně rovnice je 1, takže to vypadá na rovnici elipsy
tady je odkaz na soubor, kde na str. 7 je rovnice elipsy
a na2 = 1/4 takže a = odmocnina z 1/4 = 1/2
b na2 = 1 takže b = 1
protože b je větší než a, tak hlavní osa elipsy je rovnoběžná s osou y
střed té elipsy je v bodě [1 , -1]
tady je odkaz na př. - obecná rovnice elipsy
doplněno 17.03.20 17:13:
Buď je to A nebo D
Protože b = 1 a střed je v bodě [1 , - 1] , tak se elipsa dotýká osy x, tedy správně je A
Osy y se dotýkat nemůže, protože a = 1/2
Mezi elipsou a osou y je "mezera"1/2
----
Rovnice paraboly to nemůže být, protože v rovnici paraboly je jen jedna z neznámých umocněná na druhou, tedy buď jen x nebo jen y
Tady je odkaz na soubor, kde je to na str. 2 popsáno
Rovnice hyperboly to taky nemůže být, protože v rovnici hyperboly je mínus.
Tady je odkaz na soubor, kde je to popsáno
0x
Je potřeba tu zadanou rovnici upravit
4 xna2 + y na2 - 8x + 2y + 1 = 0
4 xna2 - 8x + y na2 + 2y + 1 = 0
4(xna2 - 2x) + (y na2 + 2y) + 1 = 0
4 (x - 1)na2 + (y + 1)na2 -4 -1 + 1 = 0
4 (x - 1)na2 + (y + 1)na2 = 4 vydělit 4, aby na pravé straně bylo 1
(x - 1)na2 + 1/4(y + 1)na2 = 1
(x - 1)na2 + (y + 1)na2 / 4 = 1
rovnice elipsy
a na2 = 1 takže a = 1
b na2 = 4 takže b = odmocnina ze 4 = 2
protože b je větší než a, tak hlavní osa elipsy je rovnoběžná s osou y
střed té elipsy je v bodě [1 , -1]
Buď je to A nebo D
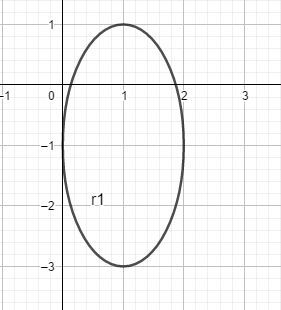
Protože a= 1 a střed elipsy je v bodě [1 , - 1] , tak se elipsa dotýká osy y, tedy správně je D
Bod dotyku s osou y je v bodě [0 , -1]
0x
Mám ještě otázku ohledně tohohle řádku:
4 (x - 1)na2 + (y + 1)na2 -4 -1 + 1 = 0 Zda-li zde ta -4 nemá být kladná? Tudíž by potom byl v pravo zápor a nevím jestli by to něco neměnilo. A ta 4 v kladu by měla být jelikož se přidala +1 a -1 ale -1 zůstala v závorce a +1 se vynásobilo 4 nebo to máte správně? Díky za odpověd ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.