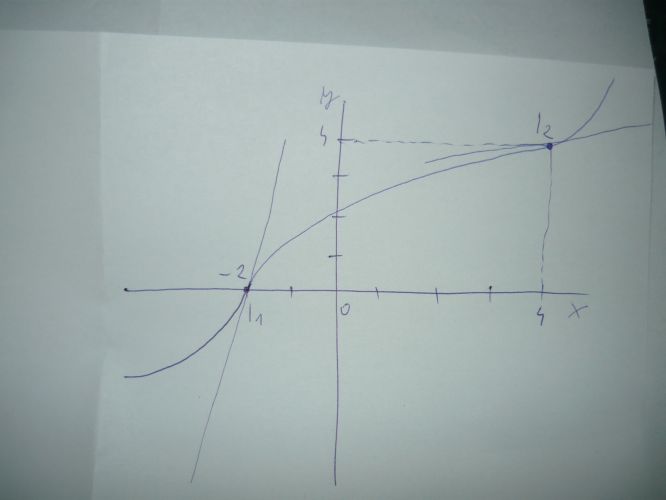
Dobrý den, jak se prosím nakreslí funkce, která je: konvexní na (-inf;-2] a [4; inf), konkávní na [-2;0] a [0;4], inflexní body f(-2) = 0, f(4) = 4, derivace f(-2) = 3 a f(4) = 1/2? Nevím, co s těmi derivacemi. Neumím nakreslit funkci, která prochází [-2;0] a má v bodě -2 derivaci 3.
Pak ještě prosím, nemohla bych někomu poslat přes vnitřní poštu víc takových příkladů jen ke kontrole?
Moc děkuji
2x
Obecně, derivace funkce v nějaké bodě je tečna grafu funkce v tom bodě. Hodnota derivace je tangens úhlu, který ta tečna svírá s osou.x. Nebo se to dá napsat tak, že derivace je směrnice té tečny. Jelikož tečna je přímka a rovnice přímky je
y = kx + q , tak hodnota derivace je to číslo k. Tedy čím větší hodnota derivace, tím víc je tečna strmá.
Tady je odkaz na soubor, kde je to popsáno na str. 4
Úhel tečny v daném bodě grafu je fí. Tangens fí je hodnota té derivace.
To je zase taková ledabylost v zacházení s pojmy. Derivace není tečna. Sice to úzce souvisí a dál to vysvětlujete správně, ale tečna je přímka, kdežto derivace je číslo (tedy pokud mlluvím o derivaci v bodě; derivaci funkce mohu definovat jako funkci, jejíž funkční hodnoty jsouy dány derivaceni v jednotlivých bodech, nerozebírám více).
2x
Dobrý den, zkuste um.mendelu.cz/...
nebo free program Graph. Jednodušší věci zvládá i aplikace Photomath.
Pro kontrolu a pochopení mi to velice pomohlo.
2x
To inf znamená možná infimum, což je nejnižší hodnota v daném intervalu. Tedy lze zvolit minimální hodnotu v oboru hodnot (na ose y) i minimální hodnotu v definičním oboru (na ose x).
doplněno 29.02.20 09:33:
Není mně ale jasný, proč je v zadání, že graf funkce je konkávní na [-2;0] a inflexní body je f(-2) = 0, což je ve stejném bodě.
Buď je v daném bodě inflexní bod a pak tam není ani konkávnost ani konvexnost, nebo tam není inflexní bod.
Není mně ale jasný, proč je v zadání, že graf funkce je konkávní na [-2;0] a inflexní bod je f(-2) = 0, což je ve stejném bodě.
Buď je v daném bodě inflexní bod a pak tam není ani konkávnost ani konvexnost, nebo tam není inflexní bod.
Už to chápu, jsou to intervaly, na kterých je konvexní nebo konkávní.
2x
Možná je to takto, jak je to na fotce
pokud
konvexnost je na int. (- nekonečno, -2 ] a na int. [4, nekonečno)
konkávnost je na int. [-2,4]
--
Pokud by tam byl ještě další inflexní bod, tak by byl v bodě [0,0], což není v zadání
Pokud byste to kreslila nějak přesněji, tak sklon první tečny k ose x je 71,5 stupňů a sklon druhé tečny (v bodě I2) je 26,5 stupňů.
Kde přesněji by mohl být ten druhý bod na ose y, to těžko odhadovat, když není zadán předpis dané funkce.
Jak se prosím vypočítají ty stupně? Co je na tom špatně?
y = 3x + q
0 = -6 + q
q = 6
tan-1(6) = α
α = 80,5°
Ten sklon tečny nezávisí na q. Ten sklon závisí jen na tom k. To q je hodnota, kde ta tečna protne osu y.
Tedy v případě té tečny v bodě I1 je to:
tan-1(3) = α
α = 71,56°
protože tan (71,56°) je přibližně 3
Dosazením do toho předpisu y = 3x + q byste spočítala souřadnice libovolného bodu na té tečně. Ale sklon a tedy úhel je jednoznačně dán tím koeficientem před x, tedy u této tečny tou trojkou.
2x
Začal bych vyjasněním pojmů. Pojem funkce a definice jejího definičního oboru definičního oboru je snad jasný. Spojitost: Ta může být definována v bodě, na otevřeném intervalu, případně obecněji na libovolné množině (vzhledem k této m noíně, ale to už je složitější a v plné obecnosti to nebudeme potřebovat). Pro spojitost a vztah k limitě platí: Funkce je spojitá v daném bodě, je-li v něm spojitá zprava i zleva; je spojitá v bode tehdy a jen tehdy, má-li v tomto bodě limitu rovn ou fun kční hodnotě; funkce má v daném bodě limitu právě tehty, má-li v něm limitu zleva, limitu zprava a tyto limity jsou si rovny. (Je.li funkce v nějakém bodě spojitá, je nutně definovaná v nějakém okolí tohoto bodu.) Funkce je spojitá na otevřeném internalu, je-li spojitá v každém jeho bodě, je spojitá na polozavřeném či uzavřeném intervalu, je-li navíc v krajním bodě (v krajních bodech) jednostrannně, tj. má-li v těcghto bodech jednoztrannou limitu rovnou funkční hodnotě.
Teď konvexnost a konkávnost: to je trochy složitější a rozlišujeme konvexnost na intervalu a konvexnost v bodě, což může úzce souviset, ale jsou to různé pojmy. Konvexnost na intervalu znamená v zásadě tolik, že graf funkce je vždy pod sečnou (názorně, "v ďolíkuú. Toje podstata tohoto pojmu, nicméně běžná definice konvexnosti předpokládá a priori, že funkce je spojitá, a toho se držme. Nicméně už z té základní definice je vidět, že konvexnost má smysl definovat jen na intervalu, ať otevřeném, polozavřeném či uzavřeném. A je-li funkce konvexní (toto vše analogicky pllatí pro konkávnost) na (a,b) a spojitá na [a,b), je konvexní i mna [a,b). Nicméně funkce konvexní nemusí být a priori hladká (tj. derivovatelná).
Konvexnost v bodě předpokládá že funkce je v tomto bodě derivovatelná; o takové funkci říkáme, že je v daném bodš konvexní (konkávní), jestliže je v nějakém okolí tohoto podu pod tečnou (nad tečnou). Ale funkce konvexní v bodě a nemusí být konvexní v žádném jeho okolí. pLATÍ ALE, ŽE FUNKCE KONVEXNMÍ V KAŽDÉM BODĚ (OTEVŘENÉHO ) INTERVALU JE KONVEXNÍ I V TOMTO INTERVALU, A NAOPAK funkce konvexní a hladná v tomto interfalu je konvexní v každém jeho bodě.
Inflexní bod se definuje pouze pro takový bod, ve kterém funkce nejen že je spojitá, ale má v něm i derivaci. ; inflexní bod je pak takový, že v malém jeho okolí levé (pravém) leží graf funkce pod tečnou a v opačném, tedy pravém (levém) okolí leží nad ní. V "rozumných" případech to znamená , že se funkce v tomto podě mění z konvexní na konkávní či naopak (i když "zvrhlý matematik" dokáže vymyslet příklad, kdy tomu tak není)-
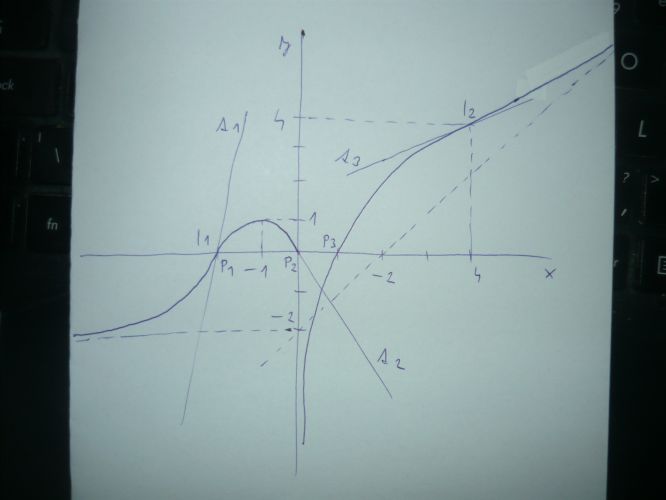
Tolik k pojmům, nějaký obrázek zkusím nakreslit a přidat extra.
P.S. omluvte případné překlepy, je to dlouhé. Zejména se omlouvám za capsLock.
Pokusil jsem se načrtnout dva návrhy. Snad se v tom vyznáte, jeden je celý černě, ten druhá má tun konkávní část nahrazenu barevnou čarou.
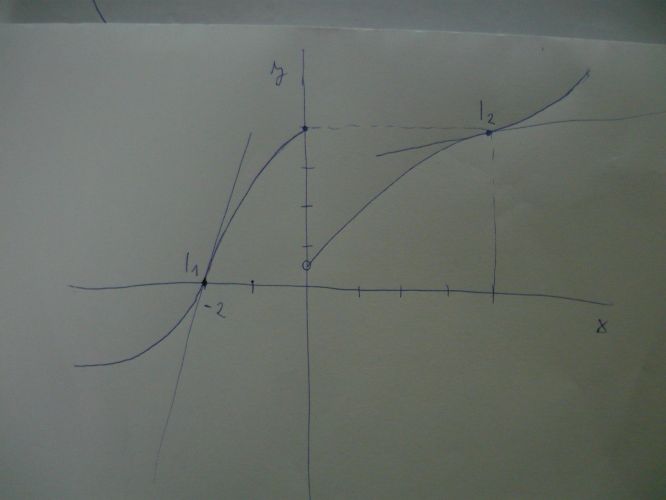
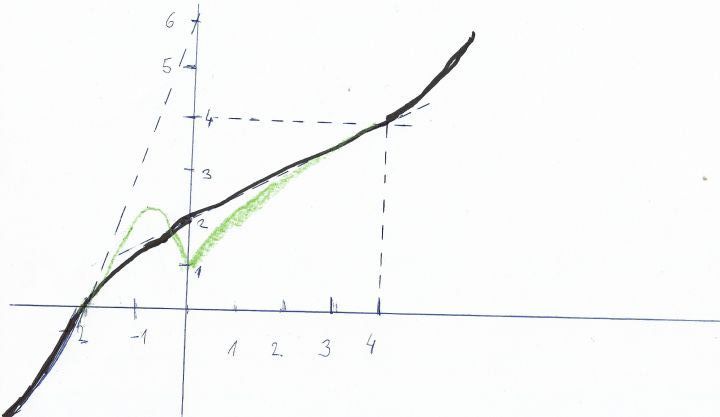
Moc děkuji a když je ta konkávní část na dva intervaly [-2;0] a [0;4], tak je tím spíš myšlena ta barevná funkce?
2x
kartaginec: Toto je obrázek kompletního zadání. Je to jeden příklad (jedna funkce), proto předtím byla ta nejasnost s intervaly. Pod tím prvním obrázkem je obrázek, kde je řešení.
Tak já nevím. Podle toho, c tazatelka psala, by tento text měl obsahovat šest nezávislých zadání. Aspoň tak mi to sdělila vnitřní poštou. Nicméně ten váš obrázek je hezký zvtipný a vyhovuje téměř všem zadáním. Ovšem trochu pochyby vzbuzuje požadavek na svislou asymptotu: to, co jste nakreslil, je jen jaednostranná asymptota. A hlavně. vaše funkce není konkávní na intervalu [0;4]. Za prvé není na tomto intervalu spojitáí, což je u konvexní funkce předpokládáno a priori, a hlavně nesplňuje definišní požadavek konkavity, totiž že pro libovolné tři body z definičního oboru, a < b < c je bot [b;f(b)] nad pod úsečkou spojující body [a,f(a)] a [c, f(c)]; stačí položit a = 0
Já si špatně přečetla zadání, proto jsem Vám to psala jinak. V tom zadání je teda asi u té konkávnosti špatně závorka - má tam být kulatá. S hranatou by to nakreslit nešlo, ne?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.