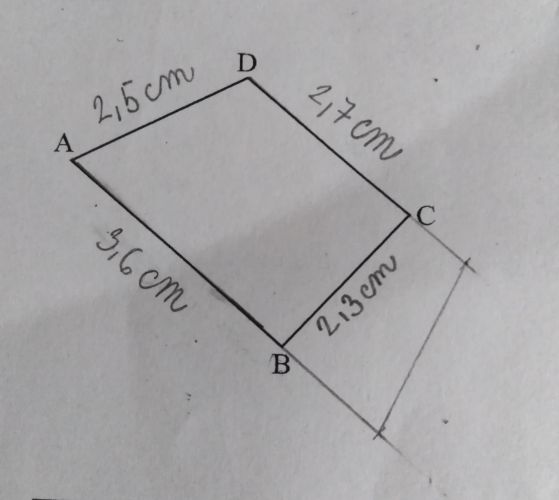
Už jsem se o to trochu pokoušela, takže v obrázku je i můj pokus, ale jsem si tím nejistá
3x
1x
Všechno je jinak.
Ono skutečně není v zadání napsáno,co se má zvětšit, jestli obsah nebo obvod, ale předpokkládal bych, že obsah.
Druhý problém ovšem je, zda se má ten obsah zvětšit "jakým,koli" způsobem tedy například prodloužením dvou stran, jak se o to pokouší zlinacci, nebo zvětšením obrázku podobností, cožje přirozenější.
Nejprve k výpočtu @zlinacci. On to myslí dobře, ale za prvé , jak ho opravil @lopezz, chtěl to zapsat tak, že jednotlivé strany prodloužil násobením 4/3 a ne jednou třetinou, ale výsledek napsal podle toho "správného" zápisu, a za druhé je jeho postup úplně blbě. Takhle by to fungovelo u obdélníka či obecněji rovnoběžníka, ale obrazec v dotaze není rovnoběžník a prostě to tak nejde. Uvědomte si, že při zvětšení těch dvou stran se změní i další strany a vše bude jinak. Skutečně, na kterém konci chce rádce ty strany prodloužit? Pokud na konci u strany AD, tam se obrazec rozšiřuje a strana AD se prodlouží. A popkud na druhém konci, tak setím naopakstrana BC zúží, tak dostaneme úplně jinýž výsledek.
Správný a nejjednodušší postub b ude sestrojit bodobný obrazec, s koeficientem podobnosti k. To znamená, že každá ze stran se zvětší k-krát, a obsah se zvětší k² krát. Takže k odmocnina za 4/3. což je přibližně1,15, prodloužená strana AB bude cca 4,15 atd.
To vše za předpokladu, že uvedený obrázek představuje původní čtyřúhelník, který máme zvětšit, a ne nejaký tazatelčin pokus.
0x
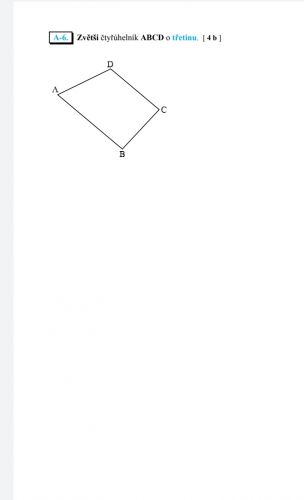
Domnívám se, že "zvětšit čtyřúhelník o třetinu" může znamenat vytvořit čtyřúhelník s daným čtyřúhelníkem podobný, s poměrem podobnosti čtyři třetiny. Pak by to chtělo narýsovat čtyřúhelník, který bude mít (při zachování velikosti úhlů, které má původní čtyřúhelník) každou stranu o třetinu větší než má původní čtyřúhelník. Obvody budou v poměru čtyři ku třem (tedy obvod nového čtyřúh. bude o jednu třetinu větší než obvod původního). Ovšem pro obsahy to neplatí! U těch je poměr 16 ku 9... Nejlepší by bylo, kdyby narýsovaný čtyřúhelník byl pravoúhlý lichoběžník (základny 3,6 cm a 2,7 cm, pravý úhel při vrcholu B a i C a výškou 2,3 cm). Zvětšení obsahu o jednu třetinu by se dosáhlo jednoduše: každou základnu zvětšit o třetinu, výšku nechat. Nejhorší varianta: jedná se o obecný čtyřúhelník a obsah nového má být o třetinu větší než obsah původního. Pak poměr podobnosti obou čtyřúhelníků by byl druhá odmocnina za čtyř třetin, což je přibližně 1,1547.Tímto poměrem vynásobit každou stranu původního čtyřúhelníka a z takto zjištěných stran při zachování původních vnitřních úhlů sestrojit nový čtyřúhelník, který bude mít obsah opravdu větší o jednu třetinu, ale věřím že tato varianta nebyla při zadání míněna... (Až po odeslání jsem si přečetl radu z 18:01...)
0x
Tak ten originální obrázek mění situaci. Ano, to, co napsal podrobně @amos, je pravda, ale v tom obrázku nejsou žádné kóty, žádná čísla, žádné délky stran, které bychom mohli násobit ať už čtyřmi třetinami, nebo odmocnnou z nich. Kde jste vzala ta čísla ve svém obrázku? To jste něco změřila? A ta čísla jsou vaše rozměry původního obrázku, nebo už váš pokus o řešení? To je teď jedno; prostě původní zadání budeme muset řešit geometricky, konstrukčně.
Tak nejprve se pokusíme řešit případ, že se má obrázek lineárně zvětšit o jednu třetinu. tedy podle amose musíme všehny strany znásobit 4/3. K tomu si pomůžeme sestrojením podobného čtyřúhelníka, nejjednodušeji stejnolehlostí.(Znáte pojmy podobnost a stejnolehlost? Napište, co o tom víte a případné neznalosti můžeme doplnit.)
Za střed stejnolehlosti bych zvolil například bod A a začal buch znásobením strany AB: sestrojil bych na polopřímce AB bod B1 takový aby vydálenost bodů AB1 (to se obvykle značí |AB1| byla tři čtvrtiny vzdálenosti AB: |AB1| = ¾|AB|. No ale jak to udělat, když žádná čísla neznáme? Jistě,mohli bychom ty délky změřit a vásledek spočítat, ale to není euklidovská konstrukce, kterou obvykle v konstrukčních úlohách vyžadujeme, i když jakázi přibližná konstrukce to je. Konstrukční řešení bude takové, že z bodu A vedeme pomocnou polopřímku AX (zvolenou víceméně libovolně, ale tak abychom následující konstrukci dokázali na papír nakreslit, aby se nám tam vešla). Na tuto polopřímku vyznačíme celkem libovolnou úsečku AX1 a tu zečtyřnásobíme: úsečku stejné délky vyznačíme z bodu X1 do bodu X2, bak s bodu X2 do bodu X3 a z bodu X3 do bodu X4. Úsečky AX3 a AX4 budou v kýženém poměru 3:4, takže teď už stačí sestrojit přímku X3B, vést s ní rovnoběžku z b odu X4 a na prúsečíky s polopřímkou AB bude kýžený bod B1.
To je yatím jen yačátek, ale já yde svůj výklad přeruším, pokuste se ho strávit, promzslete si sama, co dělat dál a oyvěte se ynovu, pak uvidíme,co s tím.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.