1x
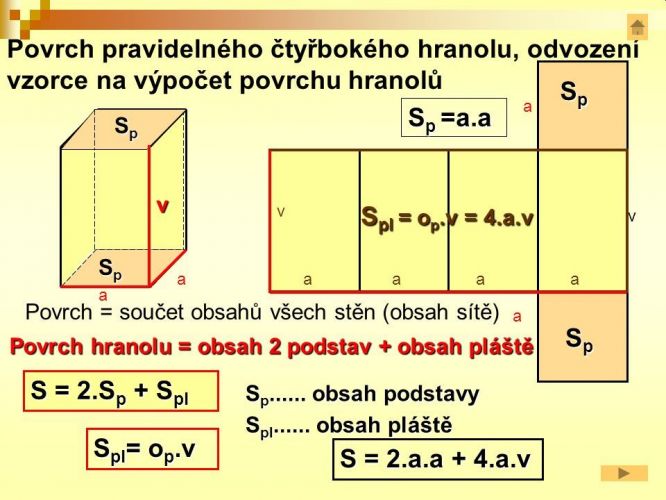
Pokud jde o příklad pro 7.ročník, míním, že je třeba chápat text "nezáludně", že každý kvádr (v tomto příkladu se jedná o zvl.případ kvádru-pravidelné čtyřboké hranoly) má plášť 20x40 cm...(Pozn.: Plášť kvádru tvoří 4 boční stěny, tedy bez podstav!). Plně podporuji řešení, které uvedl hop včera 10:09...
To, že zadání má být "nezáludné" má svúj smysl.Jen mi není jasné to o tom plášti 20x40. Možná i to bych chápal, ale jako část řešení a ne jako zadání?
V zadání příkladu je jednoznačně uvedeno, že oba kvádry mají čtvercovou podstavu. Z toho vyplývá, že plášť každého z kvádrů je tvořen čtyřmi shodnými obdélníky. U každého z kvádrů má jeho neúplná síť (bez obou podstav) tvar obdélníka s rozměry 20x40cm. U jednoho kvádru je tento obdélník rozdělen na čtyři obdélníky, každý s rozměry 10x20 cm (to jsou jeho boční stěny), u druhého kvádru jsou to čtyři obdélníky, každý s rozměry 5x40 cm (opět jeho boční stěny). Tedy bez stříhání nějakého přebytečného papíru... Z to plynou rozměry jednoho kvádru 10x10x20 cm a druhého 5x5x40 cm a další již uvedené výpočty...
Dobrý den, děkuji za odpověď. To zadání je nejednoznačné a ,,plášť obou kvádrů" jsem pochopila jako plášť obou kvádrů dohromady a to, že to může být plášť každého kvádru zvlášť, mě nenapadlo. Jsem v 9. třídě a tohle nám paní učitelka dala jako příklad na přípravu k přijímacím zkouškám, text jsem opsala přesně tak, jak to je v originále, a když jsem to tady napsala, tak už jsem potom tedy z nějakých odpovědí pochopila, že je zadání nejednoznačné a že jsem to pochopila jinak, než jsem to měla pochopit.
0x
obvod kvádrů je 5+5+5+5cm výška prvního je 20cm výška druhého je 40cm, jinak by se do papíru 20x40 nevešel a menší se do papíru samozřejmě vejde, dál počítej sám
Menší ale nebude "beze zbytku".
Já to pochopil takm že oba najednou se musí vejít beze zbytku do jednoho papíru, jinak je zadání nelogické...
Nerozumín, nechápu,nevěřím. Jednak "obvod kvádrů" je nesmysl, pokud mátew na mysli obvod základnym, tak jenom povrch bočních stran vám vychází větší než 20x40 =800, coč je obsah papíru. (vyjde 1200 cm čtverečných§.
Dobrý den, děkuji za odpovědi. Příklad jsem sem napsala proto, protože jsem příklad pochopila tak, že ,,plášť obou kvádrů" má znamenat plášť obou kvádrů dohromady, což mi samozřejmě vůbec nešlo vypočítat. Ze zdejších odpovědí už jsem potom pochopila, že bylo zadání myšleno jinak, ale je nejednoznačně napsané.
0x
1. kvádr: Výška 20cm, obvod podstavy je 40 cm, aby se vešel do papíru, takže hrana podstavy je 10cm.
Obsah postavy je 10x10=100cm2 a objem vychází 100x20=2000cm3.
2. kvádr: Výška 40cm, obvod podstavy je tedy 20cm, aby se vešel do papíru, takže hrana podstavy je 5cm.
Obsah postavy je 5x5=25cm2 a objem vychází 25x40=1000cm3
Objem kvádrů se tedy liší o 2000-1000=1000cm3=1dm3...
Dal jsem to jen z hlavy, snad je to dobře...
0x
tam je chyták, jeden kvádr má základu 10+10+10+10 =40cm obvod a je vysoký 20cm takže se do papíru vejde.bezezbytku
dtuhý má základnu 5+5+5+5=20 a je vysoký 40cm tak se vejde bezezbytku taky
Pánová, stále pokrýváte tím papírem, b oky toho kvádru. Ale k plášti patří i základny.
Jinak je otázka interpretace. Jde o to, jestli to "plášť obou kvádrů " máme chápat jako "pláště obou kvádrů dohromady" nebo "plášť každého kvádru"
@kartaginec ano, opravdu je zadání napsáno tak, že z toho nejde pochopit, zda je tím myšleno plášť obou kvádrů dohromady nebo plášť každého kvádru zvlášť. Já jsem to počítala jako plášť obou kvádrů dohromady, proto mi to nešlo spočítat. Děkuji za odpovědi a doufám, že už úkol s podobným zadáním nedostanu...
0x
Jednoduchý příklad, jednoduchá kvadratická rovnice. Jasně že na všeználky je to složité, ale učitel MFF to jistě spočítá.
Takže první kvádr má podstavu 8,28 cm a druhý 4,72 cm. Poměr objemu si snad tazatel již spočítá.
Tazatel zná jistě výsledek a neozve se, zda li má druhý kvádr objem o 480,032 cm³ menší, než první hranol
Na řešení kvadratické rovnice nemusí být učitel MF². Zdůvodnění resap. interpretace zadání je to, co vyžaduje zamyšlení.
Nepochopeno. To je příklad pro sedmou třídu. Já myslel že jeden z rádců je učitel (bývalý) z MFF a aspoň od něho se třeba dozvím, zda jsem neudělal chybu, když už se tazatel neozval.
Napadlo mne mnoho možností výpočtu, ale přes kvadratickou rovnici fakt ne... Zkus to, prosím, popsat podrobněji, dík...
Tak především. Vůbec nepředpokládám že se má hranol zabalit jak bonboniera. Jde jen o to plochu 800 cm²
Sestavíme dvě rovnicce
2x² + 4 * 20x = 800
2y² + 4 * 40y =800
Vypočteme délku postavy a snad není problém vypočítat objem.
Známe jak se vyjadřují tazatelé. Jistě by bylo lepší slovo povrch. A bez těch podstav by to asi bylo dost jednoduché. Ostatně kartaginec toho ví trochu víc a píše že podstava je součástí pláště. Frštenzi
Dobrý den, jsem žákyně 9. ročníku ZŠ a kvadratické rovnice jsme ještě nebrali. Tohle nám bylo zadáno jako příklad na přípravu k přijímacím zkouškám a opsala jsem to zde přesně tak, jak to bylo v zadání, tak nevím, co myslíte (@priklad1) tím ,,známe, jak se vyjadřují tazatelé". Příklad jsem pochopila špatně, jelikož je v zadání nejednoznačně uvedeno - plášť obou kvádrů - a z toho nejde vyčíst, jestli bylo myšleno ,,plášť obou kvádrů dohromady" nebo ,,plášť každého kvádru zvlášť". Já jsem to pochopila jako ,,plášť obou kvádrů dohromady", proto mi to nevycházelo.
0x
Musím se přiznat, že se mi tato úloha svou formulací vůbec, ale vůbec nelíbí.
Řekl bych, že je dost nepřesná. Zkusím to rozebrat.
Tak předně není úplně jasné, co znamená " Plášt obou kvádrů lze beze zbytku pokrýt papírem ve tvaru obdelníku s rozměry 20 x 40 cm", konkrétně, zda lze pokrýt plášť obou kvádrů jednim papírem, nebo zda je tím mínnplᚡkaždého z obou kvádrů. Ticméně zde bych souhlasil spíše s tím druhým předpokladem, jinam by úloha zřejmě neměla jednoznačné řešení. Kdybych jeden z kvádrů udělal dostatečně hubený, tak by zřejmě vždy zbylomísto na ten druhý dostatečně hubený-Počítat se mi to nechce, takže se hodněme na té druhé interpretaci. Nicméně malá změna zadání: plášť každého z kvádrů...by veškeré pochyby odstranila.
Takže teď máme dvě samostatné úlohu, jejichž výsledek nakonec máme porovnat, pro každý kvádr jednu.
Jistá nejasnost je i v pojmu "plášť kvádru". Jakoplášť obvykle označujeme boční část povrvhu na rozdíl od podstavy, tedy třeba u rotačního kužele ten "trychtýř" bez kruhové podstavy. Jenže co je podstava u kvádru? tozáleží na tom, jak ho postavíme, čili nazývat pláštěm boky kvádru znamená, že tento pojem není definován jednoznačně, takový kvádr bu měl podle okolností až tři různé pláště. I proto jsem sev některých svývh předchozích poznámkách klonol k tomu. yapočítat do pláště celý povrch včetně podstav. Ono se to nikde pokud vím exaktně nedefinuje, to je prostě pojem, který se užívá víceméně volně na základě dohody, která může být růyná. A protože v naše, úříkladě je vysloveně řečeno, ře podstava je ten čtverec kolmý k výšce, asi má dobré opodstatnění označit tedy jako plášť to "boční opláštění", jak to nazývá @111, Nicméně pro jistotu rozeberu i ten druhý případ, která ovšem skrývá další záludnosti.
Teď se zeptám, ro to znamená "pokrýt beze zbytku obdélníkovým papírem?" Znamená to, že nic nečouhá, nebo i to, že nic z toho papíru nepřebývá? Jinak bych tady připomněl ještě pojem "síť". Ono vlastně plášť kvádru je prostorový útvar /ať uřž ho chápeme jakkoliv) a do roviny se rozvine povrch jako síť, ty boky budou tvořit část té kompletní sítě. Pak bych to "pokrýt" mohl chápat i tak, že síť je do toho obdélníka 20x40 vepsána.
No a pak je tu ještě otázka, jestli to pokytí náhodou neznamená, že ten papír budeme muset/moci stříhat a chceme jím celá plášť polepit, aniž by zbyl kus nepolepený nebo kus nevyužitého papítu.
Tak a te%d zkusím ta řešení. Nejprve případ "nejméně záludný". Plášt je tvořen čtyřmi boky, jejichž tvar je obdélníkový o rozměrech (v prvním kvádru) 20xa, a je hledaná hranačilli strana podstavového čtverce. Pak si mohu představit, že ho rozvineme do obdélníka 20x4z, papír položíme nadvaceticentimetrivou stranou na tu výšku pláště a vyjde 4a=40, a = 14[c]. Pěkné, nezáludné intuitivní řešení. Ale co kdybych polořil ten plášť výškou na tu 40cm stranu: Pak mi sice do boků zbyde na stranu a jen 20:5 = 4cm, ale přepívá něco nahoře a podle teorie mořného stříhání kdoví, co se z toho dá udělat. Nicméně podíváme se na to takto: obsak rozvinutého pláště je 20x4a , a pokud má papír pokrýd lpášt´T beze zbytku a bez odpadu papíru,je 20x4a = 20x40 a tedy a = 10, ať to točímjakkoliv.
Dobrá, totořešení vypadá elegantně a nezáludně , a pro druhý kvádr lpostupujme amnlogicky,
doplněno 05.01.20 22:37:
No a teď ta druhá interpretace. Rovnou mohu vyloučit pokus, vepsat síťť do papíru, který selhává pro druhý kvádr: Jeho samotný plášť zabere celou širší stranu krycího papíru a na podstavy, které by k němu musely bát po straně přivěšeny, už tam není místo. Takže jen druhá možnost, celý bpovrch polepit rozstříhaným papírem.
Pro první kvádr to znamená, že povrch má hrany 20cm, a cm (a jezatím neznámá strana základnovéhu čtverce). stěny 4 krát 20xa (boky) a dvakrát axa )základny) a plochu 20x4a + 2a² = 800. To je ta kvadratická rovnice,o které mluvil prikload1 Mí tapo vykrácení tvar a² +40a - 400 a její řešení je a = -20 +- sqrt (800), vyhovuje pouze plus a řešení je a = 20(sqrt 2 -1) = (po zaokrouhlení) 8,28 cm. U druhého kvádru DOSTANEME ANALOGICKY ROVNICI a² + 80a -= 400 s řešení, a = 4,721 na 3 des. místa..
Tolikk určení kvádrů. Jejich objem a další už počítat nebudu.
@kartaginec: V zadání je uvedeno, že podstava je čtvercová, a je dána výška kvádru. Pokud tedy uvažujeme že plášť je povrch bez podstav, není řešení složité. Z toho jsem při svém postupu vycházel.
Ovšem souhlasím, že zadání není zcela jednoznačné. Není uvedeno, jestli lze papír rozstříhat a "přilepit" na jednotlivé stěny hranolu. Pro případ, že by pláštěm byl nazýván povrch hranolu, by to byla informace docela zásadní.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.