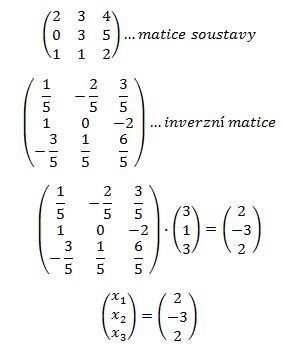Nejste přihlášen/a.
Zdravím, potřeboval bych poradit.
1) tu matici A vezmu z té soustavy? Jaký je postup?
2) u báze jsou nějaké dvě podmínky, co vím, tak by měly být lineárně nezávislé, což mi vyšlo, Takže pokud platí ještě druhá podmínka, tak by ji tvořit měly.
3) vyšlo mi 1/3, ok?
doplněno 30.12.19 13:04:
Když už jsme u těch matic, tak bych potřeboval ještě poradit s jednou rovnicí. To X mám vyjádřit jako X = -H / (G - 1)?
a ty podmínky?
0x
Báze skutečně musí být nezávislá, což Vám (správně( vušlo. Pak generuje prostor, jehož dimense je rovna počtu těch nezávislých vektotů, čili ty podmínky zde jsou, že ty vektory jsou nezávislé a jsou tři.
Tu limitu máte dobře.Ä jaký je postup u řešení? To záleží na tom? jestli existuje ta inverzní matice nebo ne. A to se pozná jak?
0x
Tady je odkaz na soubor, kde je to popsáno
Myslím si, že příklad 2 by měl být takto (ale možná se mýlím)
Když je třemi vektory tvořena báze, tak vektory jsou navzájem kolmé a třetí z nich je vektorovým součinem těch dvou
u (u1, u2, u3)
v (v1, v2, v3)
u x v = (u2 krát v3 - u3 krát v2 , u3 krát v1 - u1 krát v3, u1 krát v2 - u2 krát v1)
(2, -3, 1) x ( 2,1,-1) = (1, 4, -4)
Vektory netvoří bázi
doplněno 29.12.19 11:37:
Tak jsem se zmýlil.
Dvě podmínky existence báze jsou uvedeny zde
B je báze vektorového prostoru V, pokud platí:
⟨B⟩=V
B je lineárně nezávislá množina vektorů.
A pokud je B lineárně nezávislá, tak generuje prostor, jehož dimenze je rovna počtu těchto vektorů. No a jsou -li tři ve vektorovém prostoru V dimenze tři, pak musí (ve spojení s tou lineární nezávislostí) generovat V; obecně lze ty dvě podmínky také formulovat tak, že vektory jsou lineárné nezávislé a jejich počet je roven dimensi prostoru, v němž pracijeme. Je pravda, že tato formulace pracije se zxnalostí dimenze daného prostou, která v první formulaci číselně explicitně nevystupuje.
0x
K příkladu 2.
Matice soustavy A je matice,vytvořená z koeficientů soustavy rovnic; správně píšete, že bude mít první řádek 2 3 4, tedy bude to matice
2...3...4
0...3...5
1...1...2
(ty tečky tam píšu proto, aby se to nesmrsklo a udrželo to formátování. ) Matice, kde přidám ještě pravou stranu , tedy vektor b = 3, 1, 3., , chápaný jakosloupcová matice, se nazývá rozšířená matice soustavy. Jestliže ještě vektor proměnných x= x1,x2,x3 zapíšeme jako sloupcový vektor (sloupcotou matici se třemi řádky a jedním sloupcem), můžeme soustavu zapsat v maticovém tvaru v podobe
A*x = b.
Kmatici A může existovat inverzní jentehdy, je-li maticeA čtvercová,ale není to podmínka postačující. V našempřípadě ale existuje (matice je regulérní),jak jste se přesvědčil sám výpočtem, a pak lze řešení x (v podobě sloupcové matice) zapsat
x = A-1*b
čímž je vše vyřešeno.
(Kdyby A regulérní nebyla, platilo by tvrzení, že soustava má řešení právě tehdy, je-li hodnost matice soustavy rovna hodnosti matice rozšířené. Při hledání tohoto řešení lze použít Gaussovu eliminační metodu, která se opírá o provádění ekvivalentnívh řádkovývh úprav soušasněnamatici A anapravou stranu )tedy vlastně na matici rozšířenou) tak,abychom v matici A nakonec dostali pod hlavní diagonálu nuly. Ale v tomto případě to není třeba ~ i když je to taé možnost – a tak to nebudu rozvádět.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.