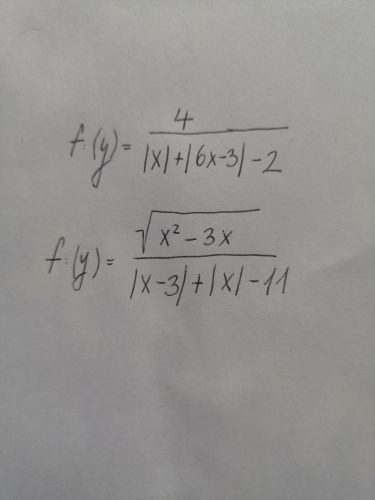Dekuji
0x
PRVNÍ PŘÍKLAD:
a)
je li x<0, tak místo /x/ napsat -x a místo /6x - 3/ napsat -6x + 3
vyřešit rovnici
-x -6x + 3 - 2 = 0
-7x +1 = 0
7x = 1
x = 1/7
výsledek je větší jak 0, takže x může být 1/7
b)
je li x větší nebo rovno 0, tak místo /x/ napsat x a místo /6x - 3/ napsat 6x - 3
vyřešit rovnici
x + 6x - 3 - 2 = 0
7x - 5 = 0
7x = 5
x = 5/7
5/7 je větší než 0, takže podmínka řešení je, že x se nesmí rovnat 5/7
Výsledek je:
D(f) = R - { 5/7 }
V zadání příkladů má být buď:
f(x) = ...
nebo
y = ...
Nemůže tam být f(y) = ... , protože nezávisle proměnná je x a závisle proměnná je y
To je pravda, má to být pro tři intervaly
Pořádně jsem se na to nesoustředil
a) pro interval (-nekonečno; 0)
b) pro interval <1/2 ; nekonečno)
c) pro interval <0; 1/2)
dopočítání za c)
je li x větší nebo rovno než 0 a současně menší než 1/2, tak místo /x/ napsat x a místo /6x - 3/ napsat -6x 3
vyřešit rovnici
x - 6x 3 - 2 = 0
- 5x 1 = 0
5x = 1
x = 1/5
1/5 je v intervalu <0; 1/2), takže výsledek příkladu je
D(f) = R - {1/5 ; 5/7 }
0x
DRUHÝ PŘÍKLAD:
a) je li x je menší než 0, tak místo /x - 3/ napsat -x +3 a místo /x/ napsat -x
řešit rovnici
-x +3 -x - 11 = 0
-2x - 8 = 0
2x = - 8
x = - 4
výsledek je menší než 0, takže x se nesmí rovnat - 4 (první podmínka)
b) je li x větší nebo rovno 0, tak místo /x - 3/ napsat x - 3 a místo /x/ napsat x
řešit rovnici
x - 3 + x - 11 = 0
2x - 14 = 0
x = 7
výsledek je větší jak 0, takže x se nesmí rovnat ani 7 (druhá podmínka)
c) výraz pod odmocninou musí být větší nebo rovno 0
spočítat kořeny toho kvadratického dvojčlenu
x na druhou - 3 x = 0
vytknout x
x krát (x - 3) = 0
jeden kořen je 0, a druhý kořen je 3
výraz je nezáporný v intervalech (- nekonečno; 0> a <3; plus nekonečno)
VÝSLEDEK PŘÍKLADU JE:
D(f) = (- nekonečno; -4) u (-4 ; 0> u <0;7) u (7; plus nekonečno)
To malé u je značka pro zjednocení intervalů
<,> jsou značky pro hranaté závorky (uzavřený interval)
- nekonečno a plus nekonečno se samozřejmě značí jako ležatá osmička, ale nevím, jak to udělat na klávesnici a fotiti se mně to nechce
Jedná se o řešení rovnic s absolutní hodnotou
Jelikož jmenovatel zlomku nemůže být 0, tak daná rovnice nesmí být rovno 0
Tady je odkaz nasoubor, kde jsou příklady řešení rovnice s absolutní hodnotou
OPRAVA:
napsal jsem výsledek druhého příkladu chybně
výsledek znova:
D(f) = (- nekonečno; -4) u (-4 ; 0> u <3;7) u (7; plus nekonečno)
Může to být napsáno i takto
D(f) = (- nekonečno; 0> u <3; plus nekonečno) - {-4 ; 7}
Taky opravuji:
To je pravda, má to být pro tři intervaly
Pořádně jsem se na to nesoustředil
a) pro interval (-nekonečno; 0)
b) pro interval < 3; nekonečno)
c) pro interval <0; 3)
dopočítání za c)
je li x větší nebo rovno než 0 a současně menší než 3, tak místo /x/ napsat x a místo /x - 3/ napsat -x + 3
vyřešit rovnici
x - x + 3 - 11 = 0
řešení rovnice není
výsledek je stejný, jak jsem napsal předtím
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.