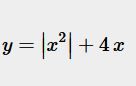Kvadratická funkce s abs. hodnotou

Jelikož x² ≥ 0, je |x²| = x² ⇒ y = x² + 4x

xx má pravdu. Takhle přímočaře v případě že rovnice řešíme v oboru reálnách čísel.Pro komplexní x nemusí být x² kladé.

Zdravím a omlouvám se včem, zejména @dominikbnp, , kterému zároveň děkuji za upřesnění.

Nejprve tedy k xx. Skutečně má pravdu, pokud pracujeme v oboru reálných čísel, což je celkem přirozený předpoklad, komplexními funjemi se zabývají vysokoškolské přednášky, Ovšem nic podstatného nebrání tomu, za x dosadit číslo komplexní a pak samozřejmě jeho úvaha neplatí.

A k mému omylu a bludu: celou dobu jsem měl zafixováno (nevím proč(, že jde o řešení rocnice 0 = |x²| + 4x. Kvadratické rovnice se i na střední škole řeší i v komplexním oboru, takže xpodobné úvahy mají smysl, a pak tedy je pravda, že řešení této rovnice usí být reálné ( a rovnice má dvě řešení, x₁ = 0 a x₂ = –4, což zjistíme mimo jiné také s uřitím poznámky xx, ovšem to je z jiné opery).