Hyperbola, elipsa, přímky

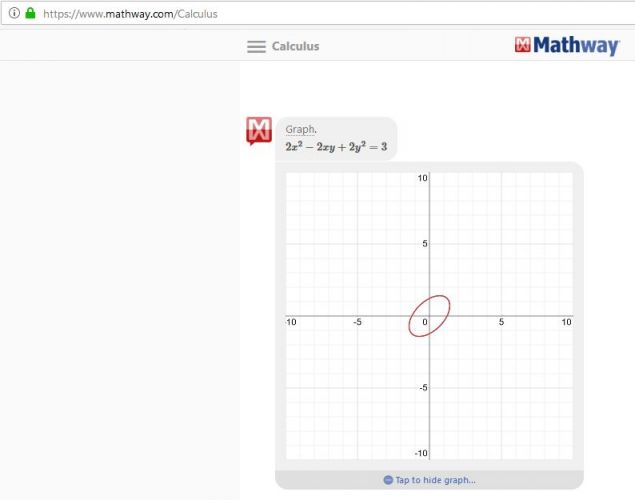
Já jsem to vyřešil dosazením do programu Mathway Calculus (jsou to obě elipsy).

Velmi zjednodušeně a orientačně:
- pokud je tam zlomek s proměnnou ve jmenovateli, je to hyberbola (y = 1/x)
- pokud je tam jedna mocnina, je to parabola (y = x²)
- pokud jsou tam dvě mocniny, je to elipsa (případně kružnice) (x² + y² = 5)

Pro upřesnění: jaká je to látka (středoškolská, vysokoškolská)?

Jinak: elipsa má základní rovnici x²/a² + y²/b² = 1, hyperbola je x²/a² − y²/b² = 1, (případně druhý kanonický tvar je x*y = k). Kdybychom na pravou stranu místo jedničky dali nulu, dostali bychom nějaký singulírní případ. Elipsa by se změnila v bod, hyperbola ve dvojici přímek. A parabola má základní rovnioci x² = 2py, pípadně y² = 2px pro parabolu s vodorovnou osou; zde má @jethropravdu. Tohle všechno jsouy kuželosečky se středem v počátku souřadnic a osami rovnoběžnými s osami souřadnic, respektive pro druhý kanonický tvar tvoří osy souřadnic asymptoty. Obecně /tedy víceméně obecně) bude mít kuželosečka rovnici ax²+2cxy +by² = 1 (pro jednoducjhost jsem vynechal rovnice , u nichž se vyskytují první mocniny x a y, které se, pokud nejde o parabolu, dají na tento tvar převést vhodnoiu substitucí. A jak teď poiznáme, kdy jde o elipsu a kdy o hyperbolu? to je otázka toho, jaké vlastnosti má kvadratická forma ax²+2cxy +by². To se dá zjišťovat například převodem na Jordanův tvar, kdy zároveň najdeme transformaci souřadnic, která rovnici převede na ten výše zmíňený základní tvar; říká vám to něco? Pokud ale chceme pouze zjistit typ kuželosečky, stačí nějak zjistit, zda je ta forma pro nenulový vektor x,y vždy kladná (elipsa), vždy záporná ( neexistuje) nebo mění znaménko (hyperbola).

Zkusím to v našem případě:

2x²- 2xy + 2y² = x²- 2xy + y² +x²+ y² = (x−y)² +x²+ y² 0 pro x²+ y²≠0 ... elipsa

Jen bych měl ještě doplnit případ, kdy je ta forma semidefinitní, což v tomto případě znamená, že je sice nezáporná (nekjladná), ale ne vždy nenulová. V takovém případě může na těch nižších mocnionách záležet, výskledkem mmůýe být parabola , alle i dvojice rovnoběžek. Například x²+2xy + y² = (x + y)² a substitucí například x+y = u, x –y = v dostaneme podobu u² a vidíme, že rovnici x²+2xy + y² = 4 odpovéídá± dvojice rovnoběžek u = ±2. kdežto rovnice x²+2xy + y² +x –y = 4 vede na parabolu u² = -(v+4).