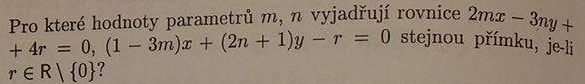Prosím poraďte mi...
mohla by mi nějaká dobrá duše napsat řešení 2 cvičení z této fotky příkladů? Velmi to spěchá...
Nevím, jak se to má správně počítat.
Řešil jsem to převedením obou zápisů rovnic na tvar y = k.x + q
Dostal jsem:
y = [ (2m)/(3n) ].x + [ 4/(3n) ].r
a
y = [ (3m-1)/(2n+1) ].x + [ 1/(2n+1) ].r
Pak jsem jen porovnal koeficienty u "x" a "r" obou rovnic (soustava 2 rovnic o 2 neznámých, respektive v té druhé rovnici bude jen "n" a jde tedy lehce vypočítat a pak jen dosadit za "n" do první rovnice).
2x
V příkladu 82 nejprve spočteme body A,B,C jako průsečíku přímek b,c, resp.c,a, resp.s,a. Obecná rovnice kolmice k přímce a:x−2u−6=0 je −2x−y=q; parametr q spočteme tak, aby vrchol A leřel na tétro přímce. Podobně si poradíme se zbylími výškami a pak vyřešíme průsečík- (Kontrola: musí vyjít stejně pro každou dvojici výšek-
1x
Ty úlohy jdou vyřešit selským rozumem při znalostech y=kx+q, grafech lineárních funkcí a sinus/kosinus pravoúhlého trojúhelníka.
Předpokládám, že při použití těch směrových tvarů přímek jsou nějaké fígle, jak to spočítat rychleji. Jestli jsem ty fígle někdy znal, tak jsem je úspěšně zapomněl, protože jsem je nikdy nepotřeboval.![]()
0x
Tak třeba u příkladu 83a máme rozhodnout, zda sysém rovnic :
.
.
.
.
2x −y = −3
x −7 = −7
3x−y = ...1
je řešitelný. K tomu lze přistoupit různě. Například lzetento systém řešit Jordanovou metodou, Nebo vyjít z podmínky řešitelnosti, která říká, že hodnost matice soustavy musí být rovna hodnosti matice rozšířené, a jelikož matice soustevy má zde evidntně hodnost dva, podmínka se redukuje na to, že determinant matice rozšířené soustavy je nulový. V každém případě zjistíme, že soustava řešení nemá. U druhého systému je to podobné, ale to jsem nepočítal.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.