0x
Co to tam máte za čísla? Ta jsou součástí zadání, nebo jste si je tam připsal?
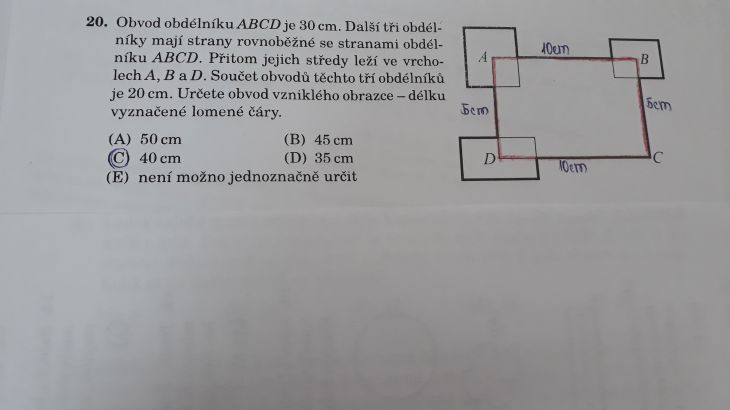
Jinak já bych řekl, že správné řešení je /B); uvědomte si, jak velkou část těch malých obdélníkú "ukousne" ten hlavní obdélník.
Tedy pokud jsem pochopil dobře, co je vyznačeno. ono je to trochu nejasné. Pokud jsem to pochopyl špatně, má pravdu Jenyk
Hehe, taky mi vyšlo 45 a když jsem viděl, že to lidem vychází 40, tak jsem to přepočítal a zjistil jsem, že jsem přičítal i ty malé ("překryté") rohy. 40 je správně.
nový_obvod = starý_obvod - (1/4).obvod_tří + (3/4).obvod_tří
Ta čísla 5 a 10cm budou pravděpodobně špatně. Při letmém pohledu na zadání se mi nezdá, že by ty délky šly vůbec určit.
I mistr tesař se někdy utne.
Myslím, že @kartaginec v rychlosti udělal stejnou chybu jako já. Rychle identifikoval 3/4 a přehlédl, že musí odečíst tu vnitřní 1/4.
Imgify: Ano, udělal jsem chybu, původ je spíš optický – na tom obrázku jsem viděl tlustou čáru kolem celého základního obdélníku a tak jsem ten rožek obdélníku nezapočítal. Ale k tomu jsem se přiznal hned v prvním komentáři.
Můj zrak není úplně nejlepší a tak jsem obrázek dešifroval nepřesně. Ano, když jsem posléze prohlédl obrázek po otevření v samostatném okně a jkeště si ho zvětšil, potvrdil jsem si svůj omyl. Ono sice na scou omluvu dodám, že lomená čára se klidně můýe křížit, to není nic proti ničemu, ale měl jsem si uvědomit (a zbystřit), že ta čára, jak jsem ji chápal dnes, se nedá nakreslit jedním tahem, jak věděl již Euler, když budoval teorii grafů.
0x
Něco chybí na malých obdélnících, to samý chybí na velkým a z toho mě vychází 40.
Ale můžu se samozřejmě plést.
Obvod obdélníku ABCD je 30cm, tazatel odvodil (2x10)+(2x5), ale může být i cokoliv, třeba (2x8)+(2x7), není to podstatné.
Součet obvodů tří menších obdélníků je 20 cm, a protože jejich středy leží ve vrcholech, musíte odečíst 1/4 (5) od obvodu obdélníku ABCD (30) a k tomuto přičíst zbylé 3/4 (15).
Výsledek je 40.
Nereaguji přímo na Jenyka, ale obecně.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.