Najdete bod na mape, ktery se nachazi 843,24 kilometru od 3. poledniku a 1234,98 kilometru od 24. poledniku. Snazim se prijit na to, jak dostat bod (nebo asi spis body, protoze muzou byt dva). Snazil jsem se najit nejaky program, ktery by mi to dokazal udelat, ale nepochodil jsem. Mohl by mi prosim nekdo pomoct, jak se dopidit toho bodu? Moc nerozumim tomu, kde zacit, protoze polednik neni jen na jednom miste.
Diky moc za pomoc.
4x
A co použít rovnou vzorec, že vzdálenost bodu se souřadnicemi s1; d1 od poledníku se zeměpisnou délkou d2 je rovna
d = R . arccos (sqrt (sin2s1 + cos2s1.cos2| d1-d2 | ) )? Samozřejmě v radiánech. To odvodíš ze vzorce pro vzdálenost dvou bodů zadaných zeměpisnými šířkami a délkami tak, že položíš derivaci podle s2 rovnou nule, a pak vyjdeš z toho, že arccos je klesající funkce, a pak upravuješ. Kdyžtak dovysvětlím.
Pro tebe teda vznikne soustava rovnic
843,24 = 6378 . arccos (sqrt (sin2s1 + cos2s1.cos2| d1- π/60 | ) )
1234,98 = 6378 . arccos (sqrt (sin2s1 + cos2s1.cos2| d1- 2π/15 | ) )
odtud
sin2s1 + cos2s1.cos2| d1- π/60 | = 0,982622
sin2s1 + cos2s1.cos2| d1- 2π/15 | = 0,962973
no a z toho mi vychází 4 body řešení, což je ve shodě s pozorováním glóbusu.
Zhruba to odpovídá těmto souřadnicím:
1) 27,5 stupně severní šířky; 11,46 stupně východní délky
2) 27,5 stupně jižní šířky; 11,46 stupně východní délky
3x
Pokud studujete matfyz, tak asi nepoužijete selský rozum a kupecké počty, ale matematiku. Pro vzdálenost dvou bodů na kouli resp. zeměkouli můžete uvažovat, že jsou na stejné rovnoběžce, nebo kdekoliv jinde a hledá se nejbližší spojnice těchto bodů, tzv. ortodoma, například při hledání nejkratší cesty pro let letadlem s ohledem na kulatost zeměkoule.
Ve vašem případě to vypadá, že zadání není úplné, ale přesto můžete udělat alespoň úvahu o možných průsečících..
1x
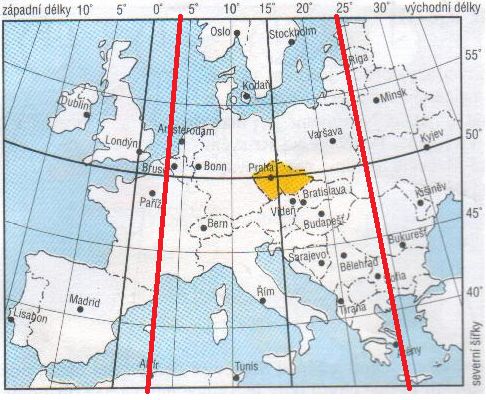
Zkuste se podívat na kulovou plochu části zeměkoule jako na rovinu jako na mapě, například na mapě Evropy a udělejte si čáru kudy vede 3. poledník a pak rovnoběžně k němu dvě rovnoběžné linie ve vzdálenosti kterou máte zadanou. Totéž se 24 poledníkem a opět dvě linie po obou stranách od něj ve vzdálenosti, kterou vám zadali ve škole. Někde by mohl být průsečík atd atd...
doplněno 16.12.18 20:48:
Není to pro výpočet, pouze pro představu, kde by hledaný bod asi tak mohl být, jestli vůbec může existovat /což je při obvodu zeměkoule 40 000 km možné/.
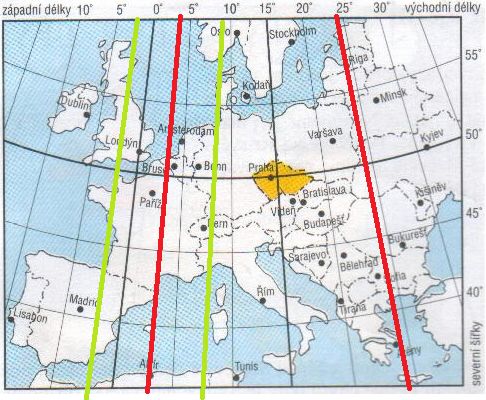
doplněno 17.12.18 10:13:
Druhý obrázek je nepřesný, linie vzdálenosti 843 km od 3. poledníku musí procházet jinými body než na hrubém obrázku. Na rovníku s průměrem 40 000 km je na 1° zeměpisné šířky 40 000 : 360 = 111,11 km/ ° atd.
Například na 45 rovnoběžce je obvod zeměkoule, neboli délka rovnoběžky asi 28 000 km a na 1° to je vzdálenost 77,78 km/ ° a například na 60 rovnoběžce to je jen 55,55km/ °.
Takže odchylka 834 km od 3. odpoledníku na rovníku je asi 7,6° což je 10,7° zem.délky. Na 60. rovnoběžce to je odchylka asi 15° plus ty 3° je si 18,7° zeměpisné délky.
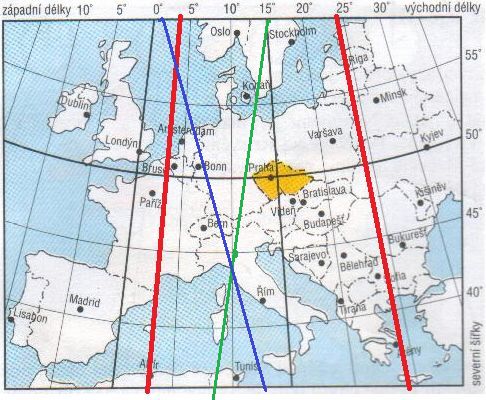
Tak můžeme stanovit body jak se zeměpisnou šířkou, tak délkou, kudy prochází linie ve vzdálenosti 834 km od 3. poledníku. Podobně se stanoví linie pro 24. poledník. (prochází body - na rovníku o asi 11,114° od 24. poledníku, tedy na 24-11,114= asi 22,23° zeměpisné šířky, na 45. rovnoběžce odchylka o 15,78°, takž linie prochází bodem 45°zem.šířky a 8,12° zem.délky, tedy asi 8. poledníkem. a na 60. rovnoběžce o 22,23° takže 24-22,23=1,7°
No a pokud jsem to nezvoral, tak by linie ve vzdálenosti 1234,98 km od 24. poledníku měla procházet těmito body. No a pak by se nakreslily obě dvě a byl by přiižný obrázk, kudy asi procházejí obě dvě a kde by se asi mohly protkout. Modrá linie na obrázku je odchylka 843 km od 3. poledníku, zelená linie ve vzdálenosti 1234,98 km od 24. poledníku.
Matfyzáci kroutí hlavou a diví se, protože oni znají naprosto přené řešení včetně započítání neforemnosti zeměkoule. Tohle je jenom úvaha
Pro nějaké orientační zjištění by tohle fungovat mohlo. Otázka je, co cíl. Pokud je cílem nalézt město do nějaké šifrovačky a na postupu nezáleží, tak by se to takhle dalo udělat. Pokud je cíl vyřešit příklad na cvičení z geometrie na matfyzu, tak tohle je použitelné jen jako náčrtek před skutečným výpočtem.
0x
Zadání není blbost, právě proto, že se poledníky sbíhají. Vzdálenost mezi poledníky je na rovníku přibližně 111 km na stupeň, na pólu samozřejmě nula. Množina všech bodů vzdálených od jednoho poledníku nějakou vzdálenost bude čára (resp. dvě čáry), která prochází rovnoběžně podél něj po povrchu Země. To samé pro druhý. Tyhle 4 čáry (respektive jen dvě z nich) budou mít někde dva průsečíky. Počítat to analyticky bude děsná fuška.
Však jste na stejném výsledku, Pletiplot píše , že vzdálenost mezi poledníky je 111 km na stupeň ( takže mezi poledníky , kterých je 360 - vzdálenost mezi nimi je jeden stupeň )
0x
Ak si predstavite poludník a od jeho každého bodu si pomyselne nakreslíte čiaru,ktorá bude kolmá,čiže rovnobežná s rovnobežkami, na ten poludník a v danej rovnakej vzdialennosti a potom tie body pospájate vyjde vám polkruh a to isté spravíte s s druhým zadaným poludníkom,tak potom by sa mali tie dva polkruhy niekde pretnúť alebo dotknúť.Predpokladám,že v geografii by na to mohol byť vzorec na výpočet.
0x
Kde jste k takové úloze přišel?
Ono, striktně vzato, na první pohled ani ten pojem vydálenosti naní úplně jasný,Mohlo by jít i o vzdálenost "v prostou", tedy třdeba i tunely, ale to moc nepředpokládám. Už proto ne, že máte hledat b od na mapš, i když ani to by nemuselo nutně být v rozporo, aale nedovedu si moc představit, jak to reálně počítat. Takže nejspíš jde o vzdálenost na globusu, což ovšem není vzdálenost po rovnoběžce. Nicméně kdybychom zadání touto podmínkou doplnili, istou cestu bych viděl. Pak by body se zadanou vzdáleností od poledníku tvořili okraj kuloového vrchlíku jehož výšku bu nebulo obtížné spočítat, Podobně by to bylo u obou polednmíků, a úloha by se redukovala na půsečík dvou kružnic. Ovšem pozor, trochu kecám, to buch hledal vzdálenost od poledníku, prodlouženého i na druhou polokouli , jako například nultého + stoosmdesátéh, v základním zadání by byly komplikace v blízkosti pólu. (A to nemluvím o tom, že země není koule, ale je šišatá.)
Ale striktně vzato, měla by to být spíše vzdálenost po hlevní kružnici, jak uvádí mhoststary. On ovšem mluví pouze o vzdálenosti mezi dvěma body, ne vzdálenost od nějaké množiny,což by byla další komplikace. Opravdu se zabýváte takhle podrobně sférickou geometrií? A nemáte alespoň nějaké omezující podmínky, třeba použití loxodromymísto ortodromy?
doplněno 16.12.18 19:18:
Možná by bylop možné vrchlík, o němž jsem mluvil, vytvořřit pomocí oprtodromy a vvýchozím azimotem devadesá nebo dvěstěsedmdesát stupňů. Skoro bych řekl, že je to cesta, ale přiznám se, že dokázat to nedovedu.
doplněno 16.12.18 20:05:
Vlastně, když o tom tak přemýšlíb, by to tak těžkmé být nemělo
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.