Nejste přihlášen/a.
1)(n/2)*(a1+an)
2) ((n-m+1)/2)*(am+an)
Nemohli byste mi prosím někdo napsat, jak postupovat krok po krůčku, abych došel ke správnému závěru? Věřím, že pro Vás to bude hračka.
Děkuji!
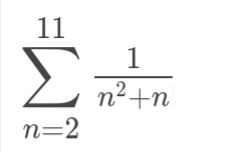
1x
Tak treba:
1/(n^2+n) rozlozime na 1/(n(n+1)) a dale pak na 1/n-1/(n+1)
Urcite vis, ze suma souctu rovna se soucet sum. Tedy muzeme zapsat:
sum(1/n-1/(n+1)) = sum1/n - sum1/(n+1), kde n=2 az 11
-
Dalsi krok lze preskocit, ale uvedu ho pro vetsi nazornost:
Řada nejde od 1 (od prvniho clenu), ale od 2. Zavedeme tedy novou promennou: i=n-1...n=i+1
a ziskavame tedy
sum1/(i+1) - sum1/(i+2), obje sumy od i=1 do 10
-
Pokud si nekolik clenu vyjadrime, rekneme od 1 do 4, ziskavame
1/2+1/3+1/4+1/5-(1/3+1/4+1/5+1/6) a po vykraceni zbyde 1/2-1/6.
A nyni uz je patrny vzorec. Prvni clen z prvni sumy zmenseny o posledni clen z druhe sumy.
V tomto pripade zapsano jako sum A1 - sum B4.
-
Konkretne Tvuj pripad (bez nahradni promenne):
sum A1 - sum Bk, kde k je n-ty clen:
sum 1/n - sum 1/(n+1), n=2 az 11...1/2-1/12=5/12.
Sice nejsem o moc moudřejší, ale děkuji za reakci! Chápu, to s tím vytknutím, respektive rozdělením na dvě sumy. Ale moc se neorientuju v tom konci. Do této rovnice "sum 1/n - sum 1/(n+1)" jsem místo prvního n dosadil 2 (chápu, jako první člen) a místo druhého n jsem dosadil 11(chápu, poslední člen). Ale co mě k tomu vedlo. To si můžu dosazovat jak chci?
Nemuze si samozrejme dosazovat libovolne.
Vtip je v tom, ze se vse navzajem vykrati krome prvniho clenu v prvni sume a posledniho clenu v druhe sume. A tedy suma od do je rozdil prvniho a posledniho clenu dosazenych do prvni, respektive do druhe sumy.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.