Kolik vody v misce zůstane?

Tak nejdříve objem nenakloněné misky - to je V1 = 2/3 * pi * r^3 jako polovina objemu koule, kde r je poloměr misky.

Po naklonění tvoří voda kulový vrchlík. Objem tohoto vrchlíku je V2 = pi*h^2 / 3 * (3r-h), kde h je výška kulového vrchlíku. Tu si musíš vyjádřit pomocí poloměru.

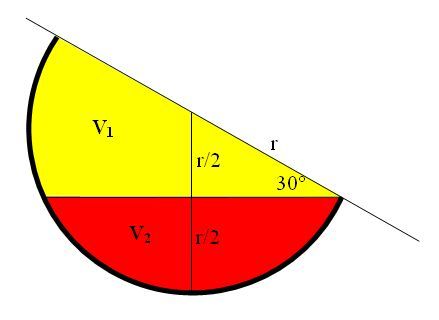
Z toho, že víš, že úhel naklonění je 60 stupňů, tak si to lze odvodit. Představ si S jako střed misky, A,B body, kde se hladina dotýká misky (bod A se dotýká vnitřku a bod B je na okraji misky, kudy voda odtekla) a bod C jako bod, kde protíná kolmice ze středu hladinu. Pak máš rovnoramenný pravoúhlý trojúhelník ASB, jehož strany AS = r, SB = r a jeho výška na stranu AB je strana SC, která měří r-h, kde h je výška vrchlíku. (nakresli si obrázek).

No a teď už jen trocha goniometrie - z pravoúhlého teojúhelníka ACS je sin 30° = (r-h)/r = 1/2, odtud

r-h = r/2,

h = r - r/2 = r/2.

Takže výška vrchlíku je v tomto případě polovina poloměru. Dosadíme za h hodnotu r/2 dp vzorce pro objem.

V2 = V2 = pi * h^2 / 3 * (3r-h) = pi * r^2 / 12 * (3r - r / 2) = pi * r^2 / 12 * 5/2 * r = 5/24 * pi * r^3

Takže rekapitulace - původní množství vody mělo objem V1 = 2/3 * pi * r^3 a zbylé množství vody má objem V2 = 5/24 * pi * r^3. Vyteklo tedy V1 - V2 = 11/24 * pi * r^3, což je 1,5 litru. A tebe zajímá, kolik vody zůstalo, tedy kolik je 5/24 * pi * r^3.

Zřejmě pokud

11/24 * pi * r^3 = 1,5,

pak 5/24 * pi * r^3 = 5/11 * (11/24 * pi * r^3) = 5/11 * 1,5 = 5/11 * 3/2 = 15/22 l vody = 0,6818... l vody.

V misce tedy zbylo 15/22 l vody, což je cca 0,6818 l vody.