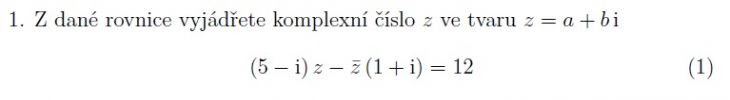Rovnice s komplexními čísly

Nechť obecně z = a+bi, kde tedy a,b jsou reálná čísla. Pak z s pruhem = a - bi. To je tzv. číslo komplexně sdružené. Dosadíme do rovnice.

(5-i)*(a+bi) - (a-bi)*(1+i)=12 ... a roznásobíme

5a + 5bi - ai - bi^2 - (a + ai - bi - bi^2) = 12 ... protože i^2=-1, dosadíme za i^2 -1

5a + 5bi - ai + b - (a + ai - bi + b) = 12

5a + 5bi - ai + b - a - ai + bi - b = 12 ... teď si sloučíme výrazy, které imaginární jednotku obsahují, a ty, které ne

5a + b - a - b + 5bi - ai - ai + bi = 12 + 0i ... 12 jako komplexní číslo lze psát jako 12+0i

4a + 6bi - 2ai = 12 + 0i

4a + (6b-2a)i = 12 + 0i ... teď jen porovnáme koeficienty

4a = 12 -> a = 3

6b-2a = 0 -> 6b = 2a = 2*3 = 6 -> b=1

tedy z = a+bi = 3+i

Odpověď: z = 3+i

@dominikpnp vám nabídl podrobný popis. Ten můj, pravda, byl dost stručný a byl to spíš jen hint; měl by stačit, Já aspoň to částečné řešením které jsem uvedl, viděl zpaměti; zkusím to rosvést,

Víte, sám nebo z odpovědi @dominikpnp, co je to komplexně sdružené číslo neboli z x pruhem, a snadno se přesvědčíte, že z plus z s prihem je reálné a z minus z s pruhem je ryze imagimární. Když teď závorky roznásobíte, dostanete jednak (vynásobenám druhého členu v obou závorkých) –i*(z+z s pruhem) , což je zjevně šíslo ryze imaginírní, a pak 5z–z s prohem,. což rozdělíme na 4z +(z – z s pruhem. Závorka je sjěvně ryze imagonární, a tedy na levé straně rovníce je jediné reálné číslo reálná část čísla 4z, řili 4x (nebo vě znaření podlla @dominikpnp 4a- Závěr je, že 4x = 12 a tedy, jak jsem avizoval a jak @dominikpnp spočítal, x = a = 3,

Dopošítávat y čili b uuž nebudu.