Nejste přihlášen/a.
Ahoj všem, Kartagincům zvlášť,
obracím se namatematicky schopnou veřejnost s dotazem, jak vypočítat následujcí limitu:
limita: x blížící se k nule
(sinx) / sin (x/2)
Děkuji za vaší trpělivost a přeji hezký den,
Tomáš
3x
Kdyz dosadime, tak by sme museli delit nulou. A to moc neumime.
Tak ja bych na to sel pres LHospitalovo pravidlo. (Snad sem to jmeno napsal dobre).
Zderivovat zvlast citatel i jmenovatel, vzniknou z toho cosinusy a tam uz se krasne da ta nula dosadit...
0x
LHospitalovo pravidlo dává správný výsledek.
Souvisí s tím ovšem drobný problém. že derivace sinu z v bodě nula se vypočte jako limita (sin x)/(x) pro x jdoucí k nule, takže musíme znát tuto limitu. Nicméně tuto limitu můžeme brát jako jednu ze základních vlastnosní funkce sinus a pak je vše v pořádku.
[Pokud byste chtěl více o této limitě, pak v této závorce něco naznačuji:
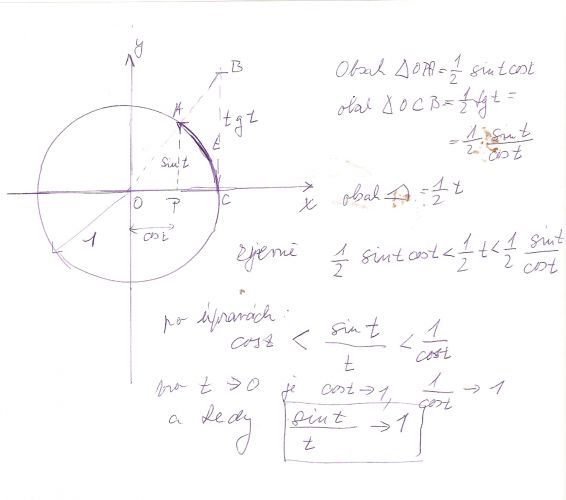
. Otázka je vtom, jak definujeme sinus. Z klasická středoškolské geometrické definice lze tuto limitu názorně odvodit (viz obrázek), má to ale z hlediska matematické analýzy své slabiny (vyskytuje se tam "zřejmě", pojem délky křivky je vlastně poměrně složitý pojem). Proto řadíme vztah lim (sin x)/(x)= 1 k základním vlastnostem..
Pak už je to Lhospitalovo pravidlo "čisté". Ale není bezpodmínečně nutné: výraz lze napsat v podobě
(sinx) / sin (x/2) = ½[(sinx) /x]/[(½x/ sin (½x)]=½[(sinx) /x]/[(z/ sin (z)], kde z= ½x jde také k nule, a použít "základní limitu".
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.