Nejste přihlášen/a.
Zdravím, potřebuji pomoct s vyřešením příkladu:
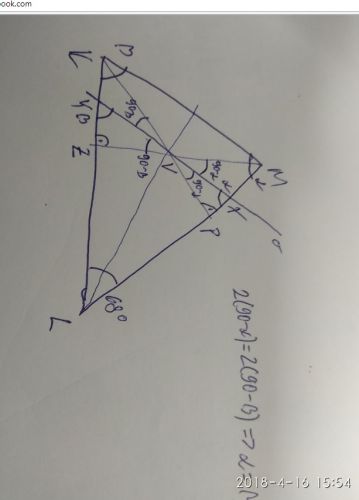
V ostroúhlém trojúhelníku KLM má úhěl KLM velikost 68°. Bod V je průsečíkem výšek a P je patou výšky stranu LM. Osa úhlu PVM je rovnoběžná se stranou KM.
Porovnejte velikosti úhlů MKL a LMK.
3x
Označ si úhel u vrcholu M alfa, úhel u vrcholu K beta. Označ si X průsečík osy úhlu PVM se stranou LM a Y průsečík této osy se stranou KL. Pak protože osa XY je rovnoběžná se stranou KM, úhel KML (alfa) se rovná úhlu YXL a úhel MKL (beta) se rovná úhlu XYL. Jde o tzv. souhlasné úhly. Trojúhelník PVX je pravoúhlý s pravým úhlem u vrcholu P, protože VP je výška na stranu LM. Pak úhel PXV je tedy alfa a dopočet do 180 stupňů říká, že úhel PVX je roven 90-slfa. Ale protože VX je osou úhlu PVM, je i úhel XVM roven 90-alfa. Podobně když si označíš patu výšky MV na stranu KL jako Z, tak z trojúhelníku VYZ vidíš, že u Z je pravý úhel, u Y je úhel beta a u V je úhel 90-beta. Tedy úhel ZVY je 90-beta a zrovna tak úhel YVK je 90-beta, protože XY je osa úhlu ZVK.
Tedy úhel PVM je 2(90-alfa) a úhel ZVK je 2(90-beta), ale jde o úhly vrcholové, tedy shodné.
Odtud 2(90-alfa) = 2(90-beta) a alfa = beta. Protože alfa + beta + 68 = 180, platí navíc, ža alfa = beta = 56 stupňů.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.