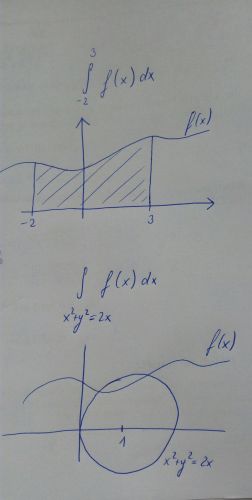
Dobrý den, co se prosím počítá za plochu, když se počítá křivkový integrál? Když je integrál z funkce a má meze, tak se počítá plocha pod tou funkcí. Ale neumím si předstvit, když je integrál přes křivku - např. kružnici? Počítá se ta plocha pod funkcí, ale nejde v ose x = 0, ale k té křivce? A když je integrál přes oblouček a jsou tam ty křivky 2? Resp. se integrál rozdělí na součet přes dvě křivky?
Děkuji
2x
Bavíme se o integrálu prvního druhu. Integruji-li jednišku (f(x,y)≡1), pak indegrál ∫ ds je prostě délka křivky, přes kterou integrujeme. Pro obecnější funkci z = f(x,y), pak integrál ∫ f(x,y)ds lze interpretovat jako obsah válcové plochy (plášť) o (proměnlivé) výšce f, "přihnuté" podle integrační křivky (představte si plot vztyčený podél té křivky). Řekl bych ale, že přirozenější je zde interpretace fyzikální. Pokud funkce f reprezentuje délkovou hustotu nějaké veličiny (pro kladné f to může být hmotnost jednotkového úseku křivky, obecněji třeba hustota náboje), pak integrál představuje celkový souhrn této veličiny (hmotnost celé křivky, celkový náboj).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.