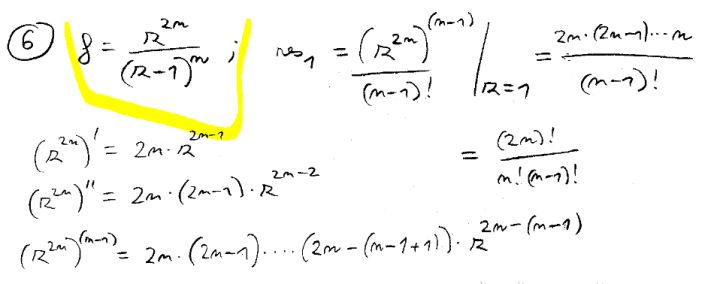Dobrý den, proč je tady prosím v tom jmenovateli faktoriál? To n v čitateli je (2n-n) a pak jsou další členu (2n-(n+1)) nebo to už končí? Děkuji
doplněno 01.04.18 10:50:
A u té derivace, proč je prosím ta jednička?
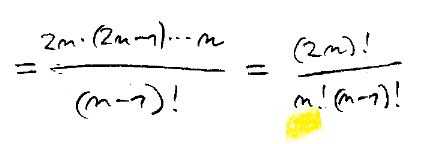
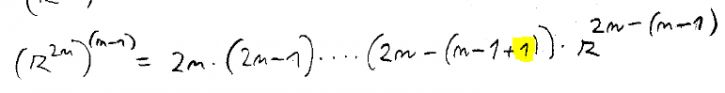
0x
Dobrý den,
nejprve bych se věnoval prvnímu problému. Mně se totiž zdá, že ta rovnost neplatí a není-li chhyba na levé straně, musí místo toho žlutého n! být (n–1!. Schválně si to rozepište pro malé n, třeba pro n = 3. Rozumím-li tomu dobře, nalevo je v čitateli součin včeh i mezu 2n a n, oba kraje včetně, a chci-li to doplnit na (2n)!. misím právě ten (n–1)! přidat a tedy na vyrovnání jím zkrátit. Takže něco je čpatně.
Možná kdybyste mohla napsat, co tomuto vzorci předcházelo, že by se nám povedlo vymyslet, co měl autor těchto výpočtů na mysli?
Já bych to viděl takto: Kdyč funkci x2n derivujete j.krát původní exponent celkem j-krát sestoupí, ovšem zároveň se v exponentu sníří o jedničku, a protože na začátku bude nezměnět a roven 2n, tak po j-tém derivováníbude snížen o j–1 a roven 2n –(j–1). A protože nerivujeme n–1 krát, vaše pochyby o té plus jedničce jsou oprávněné, j = n–1 a ta jednička není plus, ale mínus. Následně pak residuum je (2n!![]() (n+1)!(n–1)!)
(n+1)!(n–1)!)
Ono je už dost pozdě a já ještě koukal na televizi, tak to berte trochu s rezervou, já to ješt+ě skontroluji někty přes den.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.