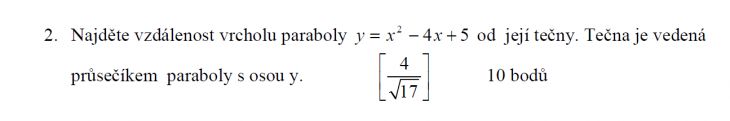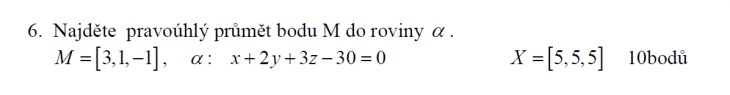Nejste přihlášen/a.
3x
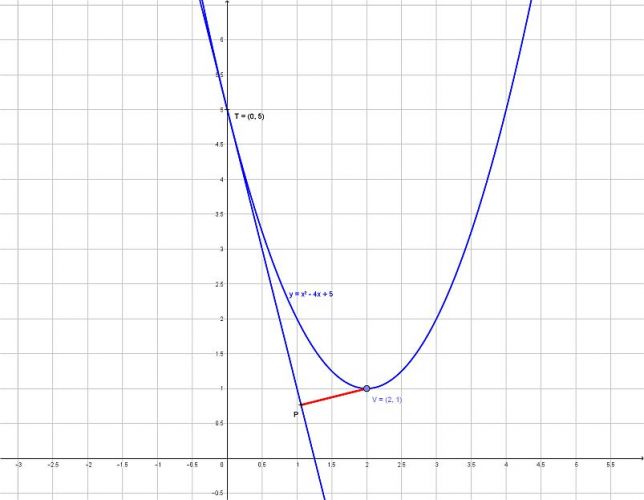
1) Nalezneme vrchol paraboly a její průsečík s osou y . Derivace v průsečíku je směrnice tečny. Vzdálenost bodu V od přímky vypočteme podle vzorce.
2) Z bodu M vedeme kolmici k rovině α. Parametrické rovnice kolmice získáme snadno, neboť její směrový vektor je normálovým vektorem roviny. Pak už jen stačí z těchto rovnic dosadit do rovnice roviny a vyřešit vzniklou lineární rovnici.
Viz první část:
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.