1x
TAkto nelze určit, záleží na rozložení hmoty tělesa. Doporučuji nastudovat moment sertvačnosti cs.wikipedia.org/...
1x
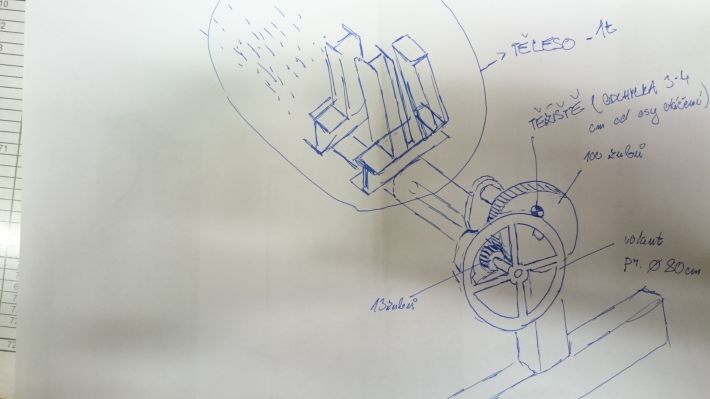
Co je "těžiště téměř v ose"? Pokud bude těžiště tunového tělesa mimo osu o 1 cm, tak tak to je moment 100 Nm a k pootočení volantem o průměru 50cm (poloměr 25 cm) budeš potřebovat obvodovou sílu 400 N, což je celkem dost. A to jsem zanedbal tření v ložiskách, které tu potřebnou sílu klidně může zvýšit dost výrazně.
OK, Dejme tomu, že odchylka osy od osy těžiště bude max 3cm, ale otáčení bych řešil převodem. Na pastorek bych připevnil volant, a pastorek by otáčel ozubené kolo v převodovém poměru cca 8, spojené s hřídelí na které bude těleso. Už bychom se bavili o rozumnějším řešení?
Opět - musíte vyjít z druhé impulzové věty, kde vystupuje točivý moment, čas jeho působení, moment setrvačnosti rotujícího tělesa a jeho konečná úhlová rychlost. Moment chcete spočítat a neznáte moment setrvačnosti, který závisí na tvaru rotujícího tělesa a ne na jeho hmotnosti. Zajisté víte, že je snazší roztočit tyč podél její osy, než kolmo k té ose.
Bojím se, že nejsem zas až takový samouk, abych byl schopen něco takového dopočítat. To těleso je svařenec různých tvarů, v některých místech je jeho odchylka od osy otáčení 700mm, v některých 300mm, v některých třeba jen 100mm a tak dále. Je posvařovaný z různých profilů. Myslel jsem, že když budu brát těleso jako celek a počítat s hmotností tohoto celku, budu schopen určit, alespoň přibližně, zda-li s ním přez výše zmíněný převod půjde otočit lidskou rukou řekněme pohodlně.
Připojuji hrubý náčrt.
Řekněme, že těleso má v místě největšího rozpětí cca 1m a hmotnost tělesa je 850 kg. Když budu tedy kroutící moment potřebný k rozpohybování tělesa počítat, jakoby těleso byl válec o průměru 1 m, dostanu hodnotu, která by měla být více než dostačující?
Dle předchozího nákresu lze spočítat ne, jak rychle svařenec roztočím, ale jakou silou ho udržím, nebo můžu otáčet. Rukou na volantu těleso klidně udržíte. Hodně záleží od vzdálenosti těžiště svařence od osy otáčení, ale to už si můžete třeba přepočítat.
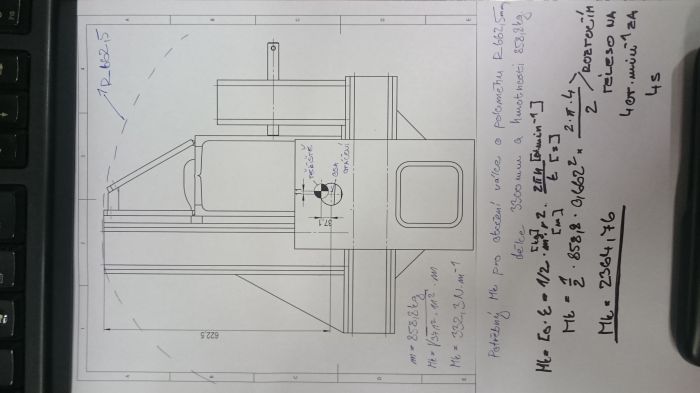
Takže, řekněme, že nebudu s tělesem otáčet rukou, ale napřímo na hřídel napojím elektromotor s převodovkou. Tím se vracím o předchozí otázce, zda-li pokud si spočítám potřebný kroutící moment k roztočení válce o poloměru R=662,5, délce 3300mm a hmotnosti 858 kg (znázorněno na výkrese v příloze) bude mi to stačit i na roztočení mého tělesa? (výsledná hodnota ve vzorci 2364 Nm mi příjde celkem dost, nemám do vzorce špatně dosazenou nějakou jednotku?).
Moment potřebný k roztočení tělesa vzhledem k vyosení těžiště jsem si spočítal (332,3 Nm). Když budu chtít poté spočítat výsledný kroutící moment k roztočení tělesa na rychlost 4 ot/min za čas 2s i za předpokladu vyosení těžiště, mám oba kroutící momenty sečíst?
Ty kroutící momenty se nesčítají, ale pomocí Steinerovy věty si přepočítáte Moment setrvačnosti pro rotaci mimo osu. Já bych k tomu ale asi přistoupil jinak - pevnostní statický výpočet, pak statický moment na volantu pro těžiště vodorovně od osy otáčení. Motor musí dávat moment vyšší, aby se těžiště nezhouplo zpět. Motor musí překonat i třecí momenty v převodech a všech ložiscích a čepech. Obávám se, že hlavně to bude rozhodovat o rychlosti roztočení.
A vlastní rotaci bych si pro kontrolu spočítal jako rotující setrvačník, který má nějakou energii, které dosáhl za nějaký čas a tedy k tomu bylo potřeba nějakého výkonu.
Mohl bych vás poprosit o nějaký konkrétní příklad se vzorečky? Obávám se, že na tohle už jsem krátký. Mimochodem, ten motor bude napojený přímo na hlavní hřídel, ten ozubený převod tam nebude.
U té Steinerovy věty mi není jasné, jak u výpočtu mmomentu setrvačnosti určím hmotné body a už vůbec netuším, jak bych měl určit jejich váhu... např. když mám na tělese navařený jekl o délce 500 mm a jeho konec je od osy otáčení vzdálený 300 mm, jak mám na jeho konci určit hmotný bod a jeho váhu.
Nebo si to celé vykládám špatně a záleží hlavně na tom kroutícím momentu potřebném k překonání vyosení těžiště vzhledem k váze tělesa? Tzn. těch mých 332,3 Nm? Takže řekněme že když nechám motor spřevodovat tak , aby na výstupu bylo řekněme 600 Nm, tak si s roztočením tělesa musí poradit bez problému?
Obávám se, že vyosení + (neznámé a klidně obrovské) třecí ztráty. A ten výpočet jako setrvačník křeba dle reseneulohy.cz/.... Ale právě že je propastný rozdíl pomalu roztočit tunové těleso se zanedbáním ztrát (třeba v beztížném stavu) a tady na Zemi, kde mohou být velké třecí odpory.
Jasně, ztráty tam nějaké budou, každopádně těleso bude uložené pouze ve dvou náklopných ložiscích, takže by neměli být bůhvíjaké. To by přece těch 250 kN navíc mělo zvládnout ne? Spíš mě zajímá to, jak se zachová ten motor... jestli s tím otočí, nebo se z něho zakouří... lépe řečeno, co je pro mě tedy pro určení jeho výstupního momentu stěžejní.
1x
jj, obávaná disciplína z technické fyziky, které říká inerciální moment setrvačnosti. Ono není až tak důležité kde je těžiště hmoty, ale jak je tato hmota rozložená. Tenkou tyčku roztočíte s menší silou, než stejně těžkou obruč. Je myslím jasné proč. Hmota obruče je rozložená na mnohem větším poloměru a proto se začnou mnohem více projevovat všechny pákové a momentové poučky.
Myslím že nemusím ani vzpomínat a sem rovnou klidně připíšu, že jestli vaše těleso má být v ose uchycená jednotunová trubka, pak s ní půlmetrovým volantem ani nehnete. A jestli platí váš náčrtek, pak mezi volantem a tělesem musíte mít šneka. Jinak vám vaše těleso rycne.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.