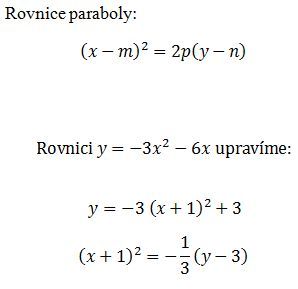Dobrý den,
nějak jsem se zamotal do hledání vrcholu kvadratické funkce y = -3x2 - 6x. Jak vypadá graf vím, ale nevím jak zjistit konkrétní vrchol.
Snažil jsem se to dělat metodou rozložení na čtverec tj. (x-3)-9 -> x = 3, y = -9 => to je, ale blbost
Můžete mě někdo popostrčit?
Děkuji
Jak by se to řešilo tou derivací eliso24? Zajímal by mě ten způsob. Jinak nejjednoduší by asi bylo použití vzorce V = [-b/2a; c - (b2/4a)].
Na derivace se používají tyhle vzorečky - na Tvou funkci se použije ten 3. řádek, tzn., že derivace y´ bude
y´ = -6x - 6
Derivace ve vrcholu je nula - má význam tečny.
-6x - 6 = 0
x = -1
V bodě -1 bude vrchol. Pak si dopočteš funkční hodnotu v bodě x = -1.
y = -3(-1)2 - 6(-1) = 3
Souřadnice vrcholu: [-1;3]
Derivace udává změnu a v tom vrcholu je ta změna nulová - funkce stoupá a pak klesá (nebo naopak), můžeš si představit, že se to tam na chvíli zastaví. Stejně jako když vyhodíš míček, tak když letí nahoru, rychlost klesá, pak je rychlost nulová (derivace je nulová) - to je to maximum, a pak začne padat a rychlost opět narůstá.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.