Nejste přihlášen/a.
Dobrý den, mám problém s jedním příkladem, přesněji řečeno nevím jak udělat "100 m dlouhý násep, jehož kolmý průřez bude mít tvar rovnoramenného lichoběžníku". Zde je příklad:
Nad vodorovným terénem se projektuje 100 m dlouhý násep, jehož kolmý průřez bude mít tvar rovnoramenného lichoběžníku. Výška náspu má být 6,5 m, šířka horní části náspu 2,3 m, úhel sklonu vytvořeného svahu má mít velikost 30°. V jaké šířce je třeba "založit" dolní část náspu?
3x
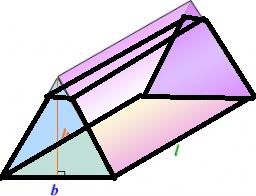
Mělo by to být vcelku jednoduché. Představte si průřez náspu sestaven z rovnostranného trojúhelníku s výškou 6,5 m a ůhly při základně 30 stupňů a zbytek bode kosod=lník o vodorovné základně 2,3 m. Spočtěte základnu trojůhelníka, přičtěte základnu kosodúlníka a je to. (Délka náspu je v tomto okamžiku irelevantní.)
Nahoře vám elisa namalovala obrázek, mohl by pomoci.
3x
Udělejte si náčrtek - rovnoramenný lichoběžník.
Jeho horní základna je 2,3 m, výška 6,5 m (v náčrtku ji veďte z vrcholu kolmo k dolní základně a můžete ji načrtnout i na druhé straně). Vznikne vám pravoúhlý trojúhelník (na druhé straně také). Znáte úhel při dolní základně lichoběžníku a výšku lichoběžníku... Použila bych funkci tg nebo cotg a vypočítala druhou odvěsnu v pravoúhlém trojúhelníku, který tam vznikl.
Dál už je to snad podle obrázku jasné ![]() .
.
doplněno 20.10.17 10:27:
Kartaginec: Nelze. Známe jen 1 stranu daného trojúhelníku.
doplněno 20.10.17 12:39:
Satam: Vážně?
Zníme dvě strany: výšku 6,5 m a přeponu 13 m (trojůhelník míúhly 30 stupňů a 60 stupňů).
doplněno 20.10.17 11:40: ad @Aknelka? Omlouvám se, blbě vydím a přehlédl jsem překlepy, tak je opravuji:Známe dvě strany: výšku 6,5 m a přeponu 13 m (trojúhelník má úhly 30 stupňů a 60 stupňů).A taky jsem to měl napsat hned k té poznámce výše. Doufám, že teď už je to dobře,
doplněno 20.10.17 11:42:
A zase mi to rozbilo odstavce!![]()
![]()
![]()
1x
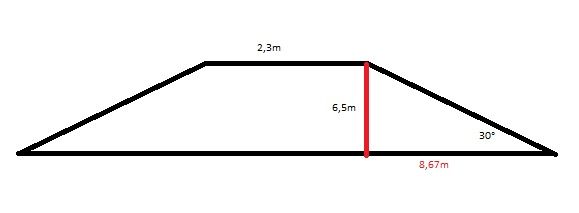
Z průřezu náspu lze "vypreparovat" klasický pravoúhlý trojúhlelník s úhly 90, 60 a 30°, tedy se stranami v poměru 3 : 4 : 5. Jednu stranu (výška náspu) známe, pak jen ani pomalu ne výpočtem, ale prostou dedukcí odvodíme "spodní" stranu trojúhleníka (6,5x 4/3 = 8,67m). Pak šířka "založení" dolní části náspu bude 2 x 8,67 + 2,3 = 19,64m.
Přikládám ilustrační obrázek bez měřítka.
Omlouvám se kartagincovi, ale nemohu s ním tentokrát souhlasit.
doplněno 20.10.17 11:53:
@kartaginec: K těm odstavcům: Rozbijou se vždy, když text uložíte s kurzorem někde uvnitř text, třeba po nějaké opravě. Nemám to ověřené na 100%, ale zatím mi to funguje tak, že když před "odesláním" textu přesunu kurzor zpět na konec textu, odstavce se nerozhodí.
doplněno 20.10.17 13:00:
@aknelka: Máte pravdu, omlouvám se, vycházel jsem z chybného předpokladu. Zde je správný výpočet:
tg 30° = 6,5/b 3-2/3 = 6,5/b 3-2b = 3x6,5 1,73b = 19,5 b = 19,5/1,73 b = 11,27
Ta základna pak bude 2x11,27 + 2,3 = 24,84m
Zároveň se omlouvám i kartagincovi, má to správně![]()
Děkji za radu s formátováním, budu na to dbát.
Ale výpočet máte špatně vy, Nevím, jak jste odvodil ten poměr 3:4:5; to jsou sice pythagorejská řísla, ale tohoto trojůhelníku se netýkají. Když už, tak strany jsou v poměru
sin 90°: sin 60° : sin 30°
(sínová věta). A kdyá se podíváte na svúi obrázek a myšlenkově ho překlopíte symetricky podle dolní základny, vidíte, že se vám vpravo udělal trojúhelník s všemi úhly šedesátistupňovými, tedy rovnostranný trojúhelník. Takže ta svislá červená strana se vám zdvojí a bude mít délku 13 cm, tutéž délku budou mít ty šikmé strany (přepona původního pravoúhleího trojúhelníka i její symetrický obraz) a díky Pythagorovi základna nebude Vašich 8,67 metrů, ale 6,5*V 3 = (po zaokrouklení)11,26 [m] (V jako odmocnina)
doplněno 20.10.17 13:02:
Tentokrát se mi to nerozhodilo (díky za radu), ale všechny překlepy jsem stejně neuhlídal. Ale snad nejsou aspoň matoucí.
Netřeba se omlouvat, hlavně ře jsme se domluvili. Já ten svůj text psal souběžně s Vaším a stejně jsem ten postub chtěl dopsat, a takhle jsem ho odeslal, až po vás. Ale zovu děkuji za radu, osvědšila se.
Jinak máme sice nepatrně odlišné výsledky, ale to je v rámci zaokrouhlení a centimetr žádná míra.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.