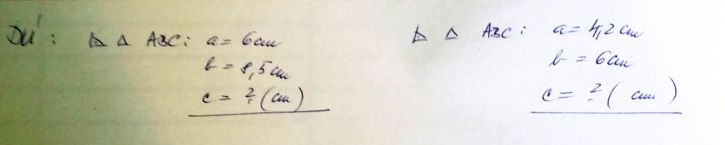Nejste přihlášen/a.
Dobrý den, potřebuji pomoct. Úkol není na známky ale chci ho splnit. Nemůžete ho prosím vypočítat a pak sem přidat foto? Úkoly jsou dva a je to PYTHAGOROVA VĚTA. Děkuji a snad mi pomůžete 
2x
Polopaticky. Pro pochopení Pythagorovy věty si narýsuj pravoúhlý trojúhelník, co má odvěsny 3 cm a 4 cm. Ta třetí, nejdelší strana je přepona. Na každou ze tří stran přirýsuj čtverec. Pro představu si čtverce rozkresli jako mřížku na centimetrové čtverečky. Na jedné odvěsně bude čtvereček 3x3 cm, to je 3 na druhou=9.
Na druhé odvěsně bude "přilepený" čtverec 4x4cm, to je 4 na druhou= 16 a na té nejdelší-přeponě vznikne čtverec 5x5cm, to je 5 na druhou=25.
Pythagorova věta zní: Obsah čtverce nad přeponou pravoúhlého trojúhelníka se rovná součtu obsahu čtverců nad oběma odvěsnami. Dosaď si z našeho příkladu 25= 9+16. A to je podstata, ze které vycházíš, jen délky stran jsou v příkladech pokaždé jiné.
0x
A kde máš v zadání. že je to pravoúhlý trojúhelník a zejména který úhel je pravý? Opravdu to je celé zadání nebo sis ho zkrátil?
Takhle mi to napsala do sešitu učitelka ale já vůbec nevím o co jde. Někdo sem napsal že a2 + b2 = c2 ale já tomu vůbec nerozumím. Nevím ani základ tohohle takže nemůžu nic počítat. Neumím to a proto to chci nechat vypočítat zde. Jinak kdybych to věděl, tak to vyhledám na netu.
Nastuduj do to, není to vůbec nic složitého a pak to dáš.
No jo, to je těřké. Takže to, co napsala pančitelka, je zkratkový zápis, ale to vám musela předtím vysvětlovat, určitě to nenapsala jen tak a včil mudruj. Tak to zkusám rozvést. Na začátku těch obou případů je takové divná znaménko; taková jakoby šipja, pčes ní oblouček a v něm tečka (tedy pokud to se svýma očima dobče vtdím,, ale nic jiného to být nemůře). Tak se označuje pravý úhel- Hned za ním je takový trojúhelníček, coč znamená, světe div se, trojúhelník. Takžr paní učitelka symbolicky napsala. JE DÁN PRAVOÚHLÝ TROJŮHELNÍK ABC O STRANÁCH a=6, B = 8,5; spočtěte stranu C
No a "n+kdo napsal", Pythagorovu věty, zase zkráceně, plně znění je že v pravoůhlém trojůhelníku popsanám výše platí. (Tedy pogud c je pčeponam a to se obvykle tak chýpe.)
Tak teď výš oč jde a uř se nevymlouvej a počítej.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.