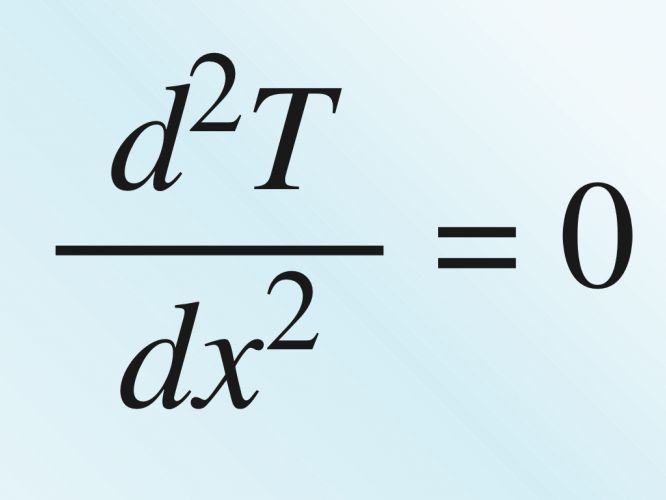Hezký večer, mohl by mi prosím někdo ukázat postup, jak se tohle na dvakrát zintegruje podle x? Prosím o postup s jednotlivými kroky. Neměla by dole zbýt x + konstanta? Ale co pak? Děkuji předem za pomoc.
tAK TŘEBA CO STUDUJETE.
Řešení je T = ½x²+bx +c; co k tomu potřebujete doplnit za postup?
doplněno 28.09.17 23:24: Samozřejmě bez toho kvadratického členu. Schválně, co řeší ten můj výraz?
Dobrý den.Tak především se chci omluvit za ten nesmyslný výsledek, který jsem napsal jako první. Já to psal ppozdě večer, byl jsem na mobilu a když jsem tu odpověď psal, neměl jsem zadání před sebou a vsugeroval jsem si, že na pravé straně máte jedničku. Takře pro jistotu ještě jednou: řešení jeT = bx +cPodrobnější výklad napíšu v klidu později. Ale stejně bych rád věděl. jak jste k této problematice a speciálně k tomuto příkladu přišel. Je to úkol ze střední školy, nebo snad z vysoké, je to z matematiky, z fyziky. nebo jste se k tomu dostal samostudiem?
Je to z knížky o teplné kondukci, T má reprezentovat teplotu a "x" v jaké vzdálonosti ve stěně. Roky jsem nepočítal žádné integrály, tak se to snažím oživit na tomto příkladu.
Děkuji, to jsem chtěl vědět.
Právě pžipravuji podrobnější odpověď, takže to zkusím vzít "od podlahy".
Takže podrobněji k otázce.
Především výraz na levé straně rovnice není vlastně "skutečný" zlomek, to je nedělitelný zymbol, označující druhou derivaci funkce T = T(x)- Místo tohoto symbolu lze napsat také T´´. nebo i (T´)´ . (Je sice pravda, že někdy s tímto výrazem zacházíme jako se skutečným zlomkem, výrazu dx , respektive dT pak říkáme diferenciál, ale já bych to raději takto neuvažoval, zvlášť když zde pracujete sdruhými derivacemi; perostě na to zapome%nte,)Z tohohle pohledu pak vaše vyjádření "Neměla by dole zbýt x + konstanta?" trochu postrádá smysl, žádné "dole" tam není a vúbec je to nějaké divné. Má to jakýsi reálný základ, ale trochu jste ho posunul-Dále, co je to zač, ta rovnice T´´=0? Na to se můžeme dívat například jako na úlohu, najít funkci F, jejíž druhá derivace je nola. A co je to druhá derivace? No to je první terivace první derivace; T´´= (T´)´ podle definice. (Taky by šlo napsatd²F/dx² = d/dx(dF/dx) ,ale tenhle můj zápis je trochu nehezký, protože jsem použil lomítek místo zlomkové čáry a tím tam zavedl zmatky, ale to by mi dělalu v tomto editoru potíže a tak se budu držet oznášení derivace čárkou, spíše z typografických důvodů.)Jestliže si nyní pro okamžik označíme (T´) = G, rozdělí se nám úloha na dva kroky:1. "řešte rovnici G´ = 0", neboli "nalezněte funkci, jejíž derivace je nulová", čili nalezněte primitivní funkci k nule, ještě jinak, G =∫ 0dx, G(x) = b,kde b je konstanta (moán byste tu konstantu raději označil c, ale budeme potřebovat ještě jednu konstantu.)2. Druhý krok bude, nalézd funkci F, jejíž první derivace je rovna gunkci G:F= ∫b dxF = bx +c, c je (další konstanta jak plyne z tabulky základních integrálů.Když už jsem tu první odpověď tak zvoral, napíšu stručně řešení rovnice T´´= 1. Na to se sice neptáte, ale například k osvěžení integrálů to může býr dobré.T´= GG =∫dx = x + bF = ∫(x+b)dx = ½x²+bx +c(Kdybyste měl zájem, mohu ještě popsat přístup k úloze jako k diferenciální rovnici;výsledek je samozřejmě stejný)
Už mi to fakt ka*ká, zas mi to zk-vilo odstavce.
Tohle je skoro nečitelné, kdyý mi editor svévolně zrušil odstavce a vůbec formátování. No nic, stejně jsem tam měl i dost vlastních překlepů, tak to zkusím znovu.
Takže podrobněji k otázce.
Především výraz na levé straně rovnice není vlastně "skutečný" zlomek, to je nedělitelný ybol, označující druhou derivaci funkce T = T(x). Místo tohoto symbolu lze napsat také T´´, nebo i (T´)´ . (Je sice pravda, že někdy s tímto výrazem zacházíme jako se skutečným zlomkem, výrazu dx , respektive dT pak říkáme diferenciál, ale já bych to raději takto neuvažoval, zvlášť když zde pracujete s druhými derivacemi; prostě na to zapomeňte.) Z tohohle pohledu pak vaše vyjádření "Neměla by dole zbýt x + konstanta?" trochu postrádá smysl, žádné "dole" tam není a vúbec je to nějaké divné. Má to jakýsi reálný základ, ale trochu jste ho posunul.
Dále, co je to zač, ta rovnice T´´=0? Na to se můžeme dívat například jako na úlohu, najít funkci F, jejíž druhá derivace je nula. A co je to druhá derivace? No to je první terivace první derivace; T´´= (T´)´ podle definice. Jestliže si nyní pro okamžik označíme (T´) = G, rozdělí se nám úloha na dva kroky:
1. "řešte rovnici G´ = 0", neboli "nalezněte funkci, jejíž derivace je nulová", čili nalezněte primitivní funkci k nule, ještě jinak,
G =∫ 0dx s řešením G(x) = b, kde b je konstanta
(možná byste tu konstantu raději označil c, ale budeme potřebovat ještě jednu konstantu.)
2. Druhý krok bude, nalézt funkci F, jejíž první derivace je rovna gunkci G:
F= ∫b dxF = bx +c, c je další konstanta (jak plyne z tabulky základních integrálů).
Když už jsem tu první odpověď tak zvoral, napíšu stručně řešení rovnice T´´= 1. Na to se sice neptáte, ale například k osvěžení integrálů to může býr dobré.
T´= G
G =∫dx = x + b
F = ∫(x+b)dx = ½x²+bx +c
(Kdybyste měl zájem, mohu ještě popsat přístup k úloze jako k diferenciální rovnici; výsledek je samozřejmě stejný)
0x
Možná jsem se rozepisoval až moc polopaticky, pokud ano, omlouvám se, ale chtěl jsem být srozumitelný.
No a teď k problému jako diferenciální rovnici. Ona to skutečně vlsatně je diferenciální rovnice, druhého řdu, ale taková ta nejjednodušší, kterou lze řešit postupmou dvojí integrací jak popsáno výše. Nicméně je to speciální případ lineární diferenciální rovnice s konstantními koeficienty, pro které platí, že mají n nezávislých řešení , kde n je řád rovnice, zde tedy dvě. Takový systém řešení nazýváme fundamentální systém (vlastně se jedná, z obecného pohledu lineární algebry, o bázi lineárního prostoru řešení, který má zde dimenzi 2) stačí tedy najít dvě nezávislá řešení α1, α2; obecné řeěení pak je
c1α1+c2α2.
Tato fundamentální řešení pak lze hledat pomocí takzvané charakteristické rovnice. Ta je motivována tak, že hledáme řešení ve tvaru α = eλx. Dosadíme-li toto hledané řešení do rovnice, můžeme výrazem eλx zkrátit a dostaneme algebraickou rovnici druhého (obecně tedy n-tého) řádu, kde místo dervace řešení dostaneme odpovídající mocninu lambda. Zde tedy má charakteristická rocnice tvar λ2=0. Taková rovnice má obecně dvě (respektive n) řešení a pokud jsou tato řešení reálná a různá, generují nám fundamentální systém.
Pokut tomu tak není, dostaneme méně řešení, než bychom potřebovali, nicméně jsou postupy, jak se k potřebnému počtu nezávislých řešení dopracovat. Nemá asi smysl popisovat tyto postupy obecně a omezím se proto na náš případ. Zde mám jedno reálné řešení λ=0, které je dvojnásobným kořenem. To nám tedy generuje jedno fundamentální řešení
α1 = e0x= 1
a v případě dvojného kořene dostaneme druho řečemí tak, že to první vynásobíme x v první mocnině; kdyby ten kořen byl vícenásobný, násobili bychom to zékladní řešení x ve druhé, třetí... mocnině:
α2=xα1 =x.
Závěr: obecné řešení je (jak už víme) F = bx+c.
Jako diferenciální rovnici bychom tu úlohu mohli řešit, i kdybychom měli na pravé straně jedničku, ale to by bylo zase o něco složitější.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.