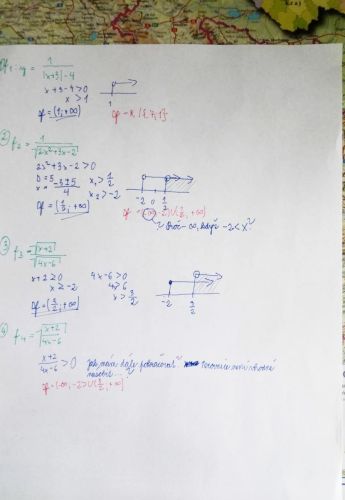1x
Tak teď trochu podrobněji.k příkladu 1.
Zde nějak nechápu, oř jste se pokoušel a jak jste přišel na ten výsledek, kterrý je "skoro dobře", def. obor je R–{−7;1}. Ta nerovnost x+3−4> 0 je vám naprosto k ničemu. Potřebujete řešit nerovnici
|x+3| − 4 ≠ 0. resp. rovnici |x+3| − 4 = 0. a její řešení z definičního oboru vyloučit. K tomu jako mezivýsledek budete řešit nerovnici x+3 ≥ 0. abyste mohl odstranit absolutní hodnotu.
U příkladu 2 máte špatně diskriminant. Následně x1 a x2 jsou řešení kvadraatické rovnice, tedy čísla, který musíte vypočítat a do žádní nerovnice je nemůžete cpát. Mezi nimi pak bude výraz pod odmocninou záporný, v nich nulový a ten uzavřený interval musíte vyloučit. Definiční obor tedy bude sjednocení dvou neomezených otevřených intervalů (kterých?)
Příklad 3 je dobře. V příkladu 4 jste začal dobře. Následně budete potřebovat, aby samozřejmě jmenovatel byl nenulový, no a aby čitatel i jmenovatel měli stejné znamonko. Takže def. obor bude sjednocením dvou intervalů: toho z řešení trojky a pok toho, kde jmenovatel je záporný a čitatel nekladný (kterýpak to bude?)
Dejte sem nyní svá doplněná řešení pro kontrolu anebo napište, je-li ještě nějaký problém.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.