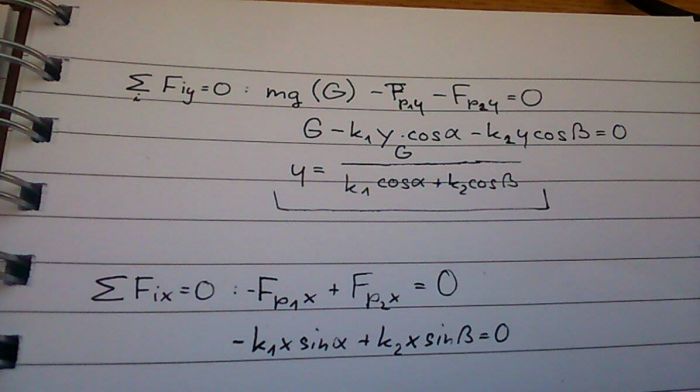Dobrý den,
potřeboval bych pomoci s jednou problematikou, mám 2 pružiny, svýrají mezi sebou tupý úhel...a kde jsou spojeny, tam jsou zatíženy silou (klasicky tíhovou) hmotného bodu. Potřeboval bych zjistit kde se pohyb ustálí.
Je zde někdo kdo této problematice rozumí a dokázal by mi pomoci?
Případně bych podal bližší informace.
Předem pěkuji,
Novák
1x
No tak snad se z těch tří sil udělá trojúhelník a spočítá se jejich velikost. Když budu znát velikost, tak z tuhosti a geometr. uspořádání spočítám délku pružin v rovnováze a z toho i polohu společného rovnovážného bodu. Protože síly nejsou konstantní a ani tvar trojúhelníka není konstantní, může to být při výpočtu dost otravné.
Nebo alternativně zkusit rozložit na dva výpočty rovnováhy sil - jeden ve směru svislém a jeden ve směru vodorovném.
0x
Já jsem totiž chtěl nejdříve zjistit, zda je tu někdo kdo tomuto rozumí.
Po zatížení břemenem m se poloha vychýlí a bod kmitá až do rovnovážné polohy.
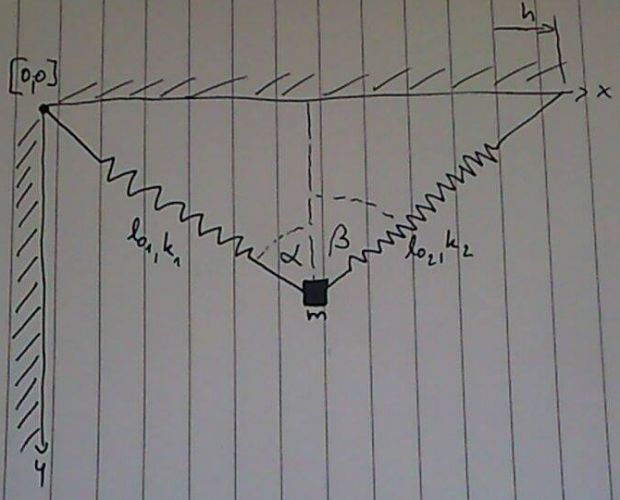
Při iteracích se potom ve směru y chová systém tak jak by se dalo čekat, ale ve směru osy x už ne...tam to lítá až moc.
x0 = 0.011,
x1 = -0.103,
x2 = 0.9550,
x3 = -8.7899
atd.
Snad je to úloha na statiku, tak jaké iterace? Ten obrázek předpokládáte už v ustáleném stavu a v ose x vyjádříte sílu od jedné a sílu od druhé pružiny, které jsou v rovnováze. A obdobně v ose y kde budou v rovnováze síly od pružin s tíhou závaží. Vyjde nějaká soustava rovnic s jedním řešením.
doplněno 18.05.17 14:57:
Nebo spíš máte říct, k jakému učivu se úloha má vztahovat. Protože řešit to jde přes statiku, ale třeba i přes celkovou energii soustavy, kde budete hledat asi její minimum při kinetické energii tělesa rovné nule.
To já jsem dělal hned na začátku, jenomže díky této podmínce mi vypadává souřadnice x...proto jsem se dostal k těm interacím.
U těch sil to je snad trochu jinak. Ty pružiny mají počáteční délku l01. Vy to počítáte, jako kdyby měly počáteční délku nulovou.
počáteční délka je l0, rovnovážná l a síla v pružině, kterou rozložíš do os je k*(l-l0). A to l si spočti z těch úhlů.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.