Nejste přihlášen/a.
Dobrý den,
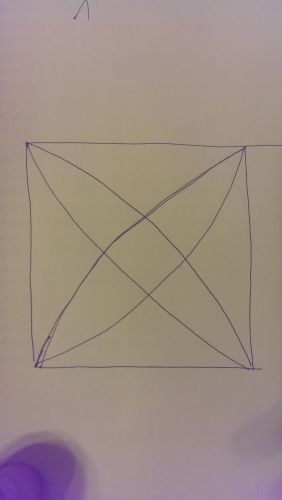
potřeboval bych poradit s jednou úlohou, řekněme, že mám zadanou měřitelnou množinu M, náhled v příloze (jedná se o jednotkový čtverec). A pomocí dvojného integrálu z 1 potřebuji nějak tento obsah propočítat.
Vím, že tato množina je rozdělena na 9 částí, z čehož 3 části stačí spočítat pouze jednou. Potřeboval bych nějak poradit s čím začít. Asi bych to měl počítat pomocí polárních ss, je to tak? Děkuji za odpovědi, Filip.
2x
Přisnám se, že ne zcela rozumím, pro jakou množinu mám ten obsah pořítat. Trochu to vypadá, že mám počítat obsah toho jednotkového řtverze, ale to je jednak truvuální a dvak nerozumím, k čemu tam pak je ta hvězdice. Asi jsem nechápavý.
Co jsem pochopil ano, máte pravdu. Podle mě je účel vytvořit integrály pro každou část zvlášť (jde o souřadnice).
Tak uplně jasné mi to stále memé, ale budiž. Možný se mají spořitat obsahy tech dílu a jako kontrola zjistit jestli dohrokady dají jedničku; tak jste to myslel? No, to je jedno; pokud bych měl spočítat ty dílčí obsahy, tak bych nejprve spočítal průseříky těch kruřnic, coř je jednoduché, a následně bych na to pustil Fubínku-
Přesně jak píšete, můžete tady prosím nastínit ty rovnice kružnic a výsledních průsečíků? Děkuji moc
Je to vcelku jednoduché. Kružnice mají středy v bodech A[0;0]ů B[1;0], C[1;1] a D[0;1]. tedy ve vrcholech čtverce. Jijich rovnice jsou (x−a)²+(y−b)²=1, kde a,b jsou souřadnice středů, tedy nuly nebo jedničky. Když dvě z těch rovnic od sebe odečteme, dostaneme lineární rovnici pro souřadnice a dosazením do rovnice kružnice snadno souřadnice vypočteme.
Pro kontrolu je jasné, že kružnice se středy v protilehlých vrcholech se protínají v těch zbylých vrcholech. a kružnice se středy v sousedních vrcholech jsou symetrické podle osy příslučné strany a tak jedna souřadnice průsečíku (která?) bude rovna jedné polovině.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.