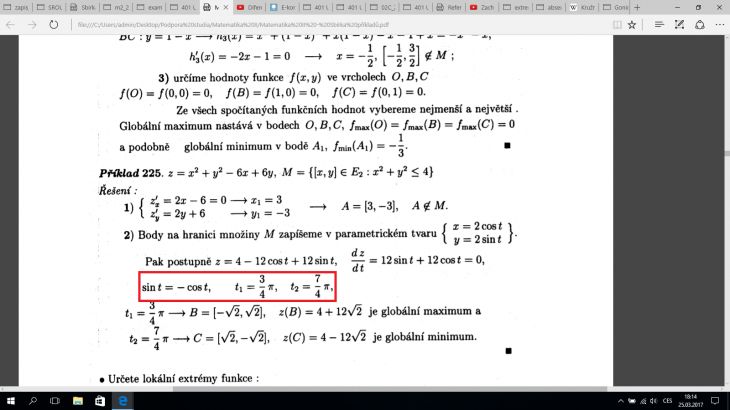
Ahoj, poradíte mi prosím někdo, jakou úvahou se dají určit ty téčka v tom červeném rámečku?
Nejjednodušší je si uvědomit, že sin 45°= cos 45°. Stejnou absolutní hodnotu nabývají tyto funkce v intervalu <0; 2π> ještě pro úhel 135° (3/4 π), 225° (5/4 π) a 315° (7/4 π). V prvním a třetím kvadrantu nabývají funkce sin α a cos α stejných znamének, ve druhém a čtvrtém kvadrantu nabývají funkce sin α a cos α různých znamének. Proto rovnici
sin t = –cos t
vyhovuje úhel ¾ π nebo úhel 7/4 π.
Dosadíme-li tyto úhly do parametrických rovnic kružnice, dostaneme souřadnice těch bodů B, C:
x= 2cos (3/4 π) = 2⋅ (–√2/2) = –√2
y=2sin (3/4 π) = 2⋅ √2/2 = √2
B = [–√2; √2]
Obdobně se získají souřadnice bodu C.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.