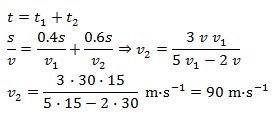prosím jak se vypočítá tento příklad
Těleso se pohybuje tak, že na prvních 40 % své dráhy má stálou rychlost ovelikosti 15 m.s1. Jak velkou rychlostí se musí pohybovat na zbytku své dráhy, aby průměrná rychlost jeho pohybu byla 30 m.s1?
0x
U podobných příkladů to mnohé svádí k představe, že průměrná rychlost bude (vážený) aritmetický průměr dílčích rychlostí. Když si ale projdete příspěvek xx, zjistíte, že v tomto případě jde o harmonický průměr, při němž průměrujete převrácené hodnoty. On se vůběc aritmetický průměr a jeho vypovídací hodnota přeceňuje. I u počítání průměrné ryvhlosti může být užitečný, pokud počítáte ne dílčí dráhy, ale dílčí časy (tedy úloha typu "40% času jízdy...", ale obecně aritmetický průměr je prostě nějak matematicky definovaná hodnota, která sama o sobě nic neznamená a teprve správná interpretace dává nějaký smysluplný a užitečný zžvěr; při zbrklé interpretaci můžete třeba říci, že když soused měl v n neděli k obědu kuře a já sušil hubu, tak jsme měli k obědu každý půl kuřete.
A ještě poznámka na okraj: tenhle výpočet vychází z implicitního předpokladu, že na zbytku své dráhy se těleso pohybovalo také konstantní rychlostí, jen jinou neý uvedeních 15 m.s−1, což vlastně v zadání explicitně řečeno není. Mohlo by se pohybovat i jinak, třeba přískoky, a pak by i výsledek byl jiný, ovšem bez bližšího určení by byla úloha neřešitelná a tak ten použitý předpoklad je docela přirozený. Jen pro zajímavost: zkuste pozměnit zadání tak, že v druhé částí dráhy se těleso pohybuje pohybem rovnoměrně zrychleným a počítejte to zrychlení. Podotýkám, že jsem to tu jen tak navrhl a sám jsem to nepočítal, ale neřešitelné to není.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.