Zdravím,
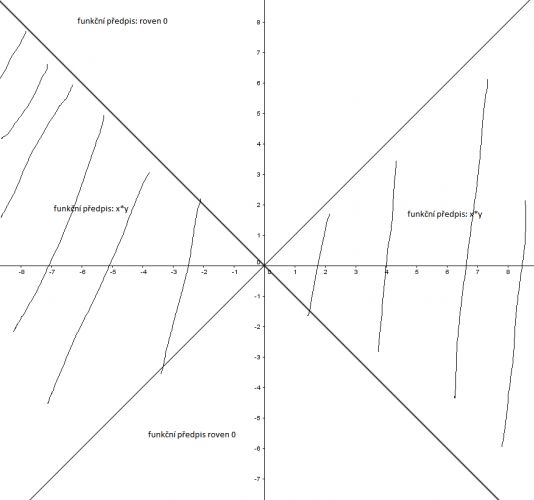
lámu si tady hlavu nad jedním slovním příkladem. Mám daný předpis funkce více proměnných, na grafu mám zobrazeno, v jakých místěch má funkřní předpis hodnoty x*y nebo popř. 0.
Dále mám dáno: f(3,2) = 6, f(2,5) = 0 (Pokud bod padne přímo na přímku/y, patří do x*1.
Mám spočítat parciální derivaci v (0,0). A ještě jsou parciální derivace různé viz níže (neplatí záměnost).
Abych se přiznal moc to nechápu, snad někdo bude mudřejší a poradí mi, děkuji všem za jakoukoliv radu.
doplněno 21.02.17 22:40:
Chybka: (Pokud bod padne přímo na přímku/y, patří do x*y).
2x
Je tp úrosté. V budě (0.0) je funkce rovna nula. Počítáte-li parciíůmé derobaci nejúrve údůe x. pak ma ose x vlastně derivujete obyčejnou derivaci podle x a ta je nulová. Dále potřebujete znát a derivovat funxi v bodech (0.y) pro y nenuloví. V okolí těchto bodů je funkce a tedy i její derivace nulová. Takže derivace podle x je na ose y nulová a její derivace podle y na celé této ose a speciálně v počátku je nulová.
Když začneme derivovat podle y, budeme tuto derivaci potřebovat znát na ose x. V počátku derivujeme podle y , při x = 0, nulovou funkci a její derivace byde nula. Ostetní body osy x leří v oblasti, kde je funce rovna x*y a jsjí derivace je rovna x. Ovřem v počátku je x ´0 a můýeme tedy číci, že na ose x je derivace podle y rovna x a derivace x úpdle x je 1. Quod erat demonstrabńdum.
Trošku mi to pomohlo, ale 100 % mi to ještě jasné není ![]() , tedy 1. par. derivace v bodě (0,0) podle y je rovna x a derivace podle x je 1 ano? Můžete mi to popř. ještě trochu osvětlit? Děkuji moc
, tedy 1. par. derivace v bodě (0,0) podle y je rovna x a derivace podle x je 1 ano? Můžete mi to popř. ještě trochu osvětlit? Děkuji moc ![]()
Není to úplné. Jde o to, že první derivace podle y je rovna x nejen v počátku, ale na celé ose x. To je důležité vědět, abyste násle¨dně mohl tuto derovaco v pořátku derivovat podle x a dostal , že druhý derivace v počítku (a nejen v něm zle v ostatních bodech osy x nám už to bude jednoúm počátaná v pořadí nejprve podle y a pak podle y je rovna jedné. No a první derivaci podle y musíme znát nejen v počátku, ale na celé ose y, z podobných důvodú. Už stači?
Nojo, ale definoce funkce z, kterou jste uvedl v zálaví vašeho řešení, neodpovídá úvodnímu nákresu. Ta definice z rukou psaného dextu odpovídá funkci f(x,y) = xy všude a taková funkce ovšem má druhé derivace záměnná Uvodní definice je
f(x,y) - x*y pro |x| ≤ |y|
f(x,y) = 0 pro |x|> |y|
(f(0,0)=0 už je vlastně redundantní)
Jasně díky, jen nevím jak to teď pojmout a zapsat. Jak by v celkovém souhrnu vyšly tyto druhé parc. derivace, když budou různé? Děkuji
To jsem se snažil cvakrád různě podrobně napsat, skoro už nevím, co k tomu dodat. Můžete mi napsat, řemu konkrétně nerozumíte, abych to mohl zkusit vysvětlit?
Snad jen přehledně: K výpočtu druhé derivace (podle x, podle y) potřebyjete tu první derivaci (podle y, podle x) znát na ose (ose x, ose y); pak už ji počítáte jako obyčejnou derivaci.
Vraťme se ke vstupnímu definičnímu obrázku:
Uvnitř vyšrafované oblasti je f(x,y) = x*y a derivaci pro všechny body v ní, speciálně pro body oxsy x mimo počátek, spočteme snadno.
Vně této oblasti je f nulová a derivace pro body v tom vnějšku, zpeciálně pro body osy y mimo počátek, spočteme ještě jednodušeji.
Derivace v počátky tedy musíme spočítat extra, jak, to jsem se pokusil popsat.
No a pak už by to mělo být opravdu jednoduché.
Jsem úplně ztracen, asi polopatě odzačátku nebo nevím. Jsem zvyklý vycházet z předpisu fce. A nechápu jak mám dostat v počátku par. derivace 2. řádu rozdílné. Jestli to mám udělat úvahou nebo jinak
Napíši co chápu:
Když počítám parc. derivace podle x, tak nahlížím na y jako na konstantu. Tato derv v bodě (0, y - hybu se po y ose), kde y je je ruzne do nuly. A derivace podle x v (0, y) je tedy podle nákresu rovno 0.
Když derivuji podle y, tak na x nahlížím jako na konstantu, tedy dá se říct, že ji zjištuji na ose x (defacto. přímky rovnoběžné s osou x). A tam je kromě bodu (0,0) první der. rovna y (deriv. podle y v (x, 0)?
doplněno 08.03.17 22:28:
Snad už to bude úplné:
1. derivace podle x na ose x se rovná 1, kromě počátku
derivace podle x na ose y se rovná 0 na celé ose.
2. derivace podle y na ose x se rovná x, kromě počátku
derivace podle y na ose y se rovná 0 na celé ose.
Už to je lepší? z každé této situace mám vyjít pro výpočet 2. deriv? Díky moc ![]()
Asi tekhle: když derivuji podle x, skutešně na y nahlíčím jako na konstantu. Tato konstanta ovčem můýe být kdekoli v defoničním oboru funkce f, ale ne pro každá y existuje. Pokud je bod (x,y) v ublasti nevyčárkované (tedy uvnitř těch nevyčárkovaných prostor), je f rovna nule a derivace nuly je nula. Je-li ovšem (x,y) uvnitř vyšrafované oblezti, je funkce f rovna x*y a derivace podle x je rovna y. pokud je ovšem bod (x.y) někde na tech dvou osách kvadrantů, je situoce složitější, Prozradím bám, že mimo počátek derivace podle x ani podle y neexistuje, ale nemusíte se tím zabívat podrobneji, tam nás nebuce zajímat, ale v počátku ji potčebovat budeme, o tom pohovoříme později třeba zítra; zatím se nat tím zamyslete. Podobné je to s derivací podle y, zkuste si to promyslet. Je pravda, že tředba derivace v bodě (4,9) nám nebude k ničemu, nicméně zatím si to promyslete v obecnosti, zkuste počítat první derivace i v počátku, Jinak je už pozdě, nashledanou později.
Teď bych to tedy zkusil podrobněji.
Naším cíklem je vypočítat smíšené derivace v počátku. K tomu potřebuji znát derivaci podle y na ose x včetně počátku, abych ji pak mohl vyšetřovat jako funkci proměnné x (y beru konstantně nulové), a derivovat ji podle x; tím dostanu zmíšenou derivaci nejprve podle y a pak podle x.
Správně píšete, že
2. derivace podle y na ose x se rovná x, kromě počátku
derivace podle y na ose y se rovná 0 na celé ose. (tedy speciílně i v bodě (0,0).
No jo, ale v počátku je x = 0, takže řeknete-li, že derivace podle y se v počátku rovná x, máte pravdu. Shrnuto: derivace podle y se na celé ose x včetně počátku rovná x. A co potřebujeme znát? Derivaci funkce f podle y, , následně zderivouvanou podle x, a to konkrétně její hodnotu v počátku. A jak ji spočteme? Zjistikli jsme, že derivace f podle y se na celé ose x rovná x, a derivace podle x z výrazu x je rovna jedné opět na celé ose x a tedy i v počátku.
=================
Tak a teď budeme derivovat nejprve podle x a následně podle y, chceme najít hodotu v počátku. K tomu musíme najít nejprve derivaci f podle x na ose y včetně počátku, kterou následně zderivujeme podle y při x pevném, rovném nule, a do výsledku dosadíme y = 0 (tedy x=0, y = 0, což je počátek). Podívejme se, co jste napsal:
1. derivace podle x na ose x se rovná 1, kromě počátku
derivace podle x na ose y se rovná 0 na celé ose.
Ten druhý řádek je správně, a když tedy tuto nulovou funkci (při pevném x rovném nule) zderivujeme podle y, vyjde nulavčude na ose y, tedy i v počátku. Takže jsme zjistili, že smíšená derivace fce f v počátku závisá na pořadí, Začneme-li derivovat podle z, vyjde nula a začneme-li derivovat podle y, vyjde1.
Problém je ovšem v tom, že mi není jasné, jak jste zjistil, že "derivace podle y na ose y se rovná 0 na celé ose." Pravda to je, ale ta první číst, totiž "2. derivace podle y na ose x se rovná x, kromě počátku" je nesmysl a nechápu, jak jste na to přišel, Přece funkce f¨(x,y) je na ose x rovna nule; od kdy je derivace nuly je rovna jedné? Spráná úvaha je taková: derivace f podle x je rovna nule všude na ose y krom počátku, protoče tyto body leží uvnitř oblasti kde je f nulová, dále je rovna nule včude na ose x, tedy i v pošítku, a jako závěr vyjde to, že ta derivace je rovna nule na celé ose y všetně počátku.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.