Dobrý večer, procvičuju si exponenciální funkce a nechápu, jak mám vypočítat tady tento příklad. Jak mám vypočítat všechny hodnoty, aby tato funkce byla rostoucí? Potřeboval bych postup, abych dokázal další příkady vypočítat samostatně. Předem děkuji za jakoukoliv radu. 
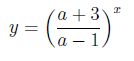
1x
Exponenciální funkce ax je roustoucí, pokud je a>1 (z intervalu (1;inf))
Začni tedy tím, že
(a+3)/(a-1)>1
doplněno 22.02.17 06:32:
Řešíš nerovnici (a+3)/(a-1)>1 a z podmínky a<1 víš, že jmenovatel nebude záporný, proto můžeš zlomek vynásobit kladným číslem (a-1) aniž by se změnilo znaménko nerovnosti
a+3>a-1
a>a-4
a to platí vždy
Výsledek je tedy, že funkce je rostoucí pro a z R
Děkuji, nicméně toto sjme si taky našel, že to musí být větší než 1. Ale nevím,jak mám s tím postupovat 
Bohužel, i tak jsem to nepochopil, jak to mám udělat. Nemůžete mi prosím někdo vypočítat vzorový příklad? Mám tu hodně příkladů na procvičení, takže bych to chtěl umět, abych to dokázal vypočítat. Děkuji.
Ten příklad jsem vypočítala celý.
V tom příkladu jde jen o to, že rostoucí funkce je exponenciální, když je funkce větší než jedna a pak se vypočítá nerovnice.
Tak sem dej další příklad.
Takže řešení by vypadalo takto:1.) Nutná podmínka je a ≠ 1.2.) Pro a> 1 lze nerovnici násobit a −1 beze změny smyslu nerovností a dojdeme skutečně k nerovnosti a> −4. Ta je skutečně splněna pro každé reálné a,3.) Pro a menčí než jedna dojdeme k nerovnici a+3doplněno 06.03.17 15:46:
Ta ovčšem neplatí nikdy. Závěr:
Zkoumaná funkce je rostoucí pro všechna a větší než jedna,
Jinak, zase mi to editor totálně zmrvil a v pětiminutovém termínu jsem to nestačil všechno opravit. Zkusím to rozdělit.
doplněno 06.03.17 15:47:
Ta ovčšem neplatí nikdy. Závěr:
Zkoumaná funkce je rostoucí pro všechna a větší než jedna,
Jinak, zase mi to editor totálně zmrvil a v pětiminutovém termínu jsem to nestačil všechno opravit. Zkusím to rozdělit.
No já tomu taky nerozumím, z předložených výpočtů.Především se mi moc nelíbí, že je zde písmeno a použito ve dvou významech, jednak jako základ exponencíáli a jednak jako a ze zadání. To může vnést do uvažování trochu zmatek, rtakže bych raději napsal
Exponenciální funkce bx je rostoucí, pokud je b>1
Následně bych položil b = (a+3)/(a-1) a řešil bych (s tím už souhlasím) nerovnici
(a+3)/(a-1)1.
Zde ovšem žádnou apriorní podmínku a menší 1 nevidím. (Neměla Elisa na mysli a větší jedné? Tvrzení, že proto je a− 1 kladné, by tomu odpovídalo, ale ani tuto podmínku zde apriorně nevidím; není to způsobeno právě tím dvojím onačení, o němž jsem mluvil
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.