Ahoj, pomohl by mi tu někdo vypočítat tyto dvě rovnice? Zasekl jsem se hned u té první, rozložil jsem jí na (8!/(x!*(8-x)!))=(8!/(5!*(8-5)!)) a myslel si, že to půjde třeba nějak vynásobit, vůbec ale netuším, jak postupovat. Díky ![]()

2x
a) Vždyť jen porovnáním je jasné, že x = 5.
b) Úpravou vztahu ne levé straně dostaneme 7 nad x+1 a porovnání máme x+1 = 4.
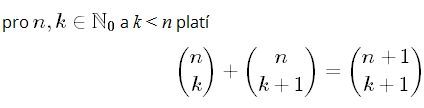
Děkuji za reakci, ale bohužel mi to stále není jasné, můžete příklad podrobněji rozepsat? Děkuji ![]()
Jak vzpadají kombinační čísla? n nad k je z definice rovno n!/((k!)(n−k)). Z toho vidíte, že n nad k je totéž jako n nad (n−k).
No, že rovnost n nad k = n nad 5 (například) spňuje číslo x = 5, jak upozorňuje @x, je snad jasné, ne? Takže první příklad má minimálně dvě řešení, totiž x = 5, a dle mého doplnění ještě 8−x = 5 čili x = 3. Jiné řešení už není, to už si rozmyslete sám (představtesi třeba Pascalův trojúhelník.
No a když v příkladu 2 použijete vzorec, který vám poradil @x, převedete ho vlastně na příklad 1; jestli to nevidíte, tak se zamyslete (nad příkladem i nad sebou); uvedený vzorec se dokazuje v teorii kombinačních čísel a můžete ho brát jako známý fakt.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.