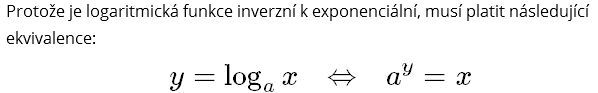Nejste přihlášen/a.
Dobrý den, bereme logaritmy a nebyla jsem si schopná poradit s tímto příkladem:
log(3x −8) = 2−x
Ten logaritmus má být o základu 3.
Můžete mi pomoci?
Děkuji
doplněno 12.02.17 18:24:
A potom si ještě nevím rady s tímto:
x^(logx) = 10 000
doplněno 12.02.17 18:44:
Ten druhý už mám
0x
Tak na řešení si taky rád počkám, protože úpravami se k ničemu lepšímu než x.kx nedokážu dobrat ![]()
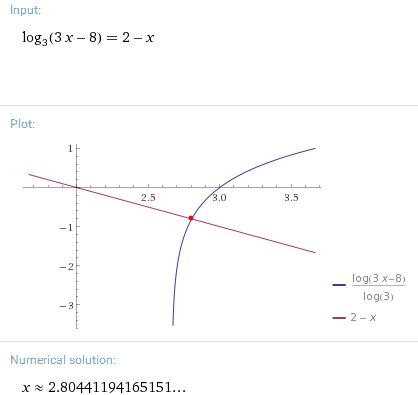
Z grafů mi jen vychází, že x vyjde něco mezi 2,67 a 3.
WolframAlpha souhlasí.
0x
Možná je v tom zadání překlep?
Kdyby bylo: log3(3x-8) = 2-x
tak to vyjde lehce a hezky x=2
![]()
Ano, omlouvám se, nedala jsem si pozor. Mělo to být tak, jak to píšete. Ale jak se k tomu dopracuji?
Z definice logaritmu (případně obě strany rovnice převézt do exponentu mocniny):
3X-8 = 3(2-x) (přes to povýšení do exponentu mocniny: 3log3(3^x-8) = 3(2-x) )
3x - 8 = 32/3x ; vynásobit obě strany 3x
3x.3x - 8.3x = 9
(3x)2 - 8.3x - 9 = 0
substituce: y = 3x
y2 - 8y - 9 = 0
kvadratická rovnice s kořeny: y1 = -1 a y2 = 9
3x = -1
x = log3(-1) ... nedefinován
3x = 9
x = log39 = log332 = 2.log33 = 2.1
x = 2
doplněno 13.02.17 20:11:
Pomalu píšu - @x mě předběhl ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.