můj dotaz spočívá ve vzorci na výpočet objemu jehlanu (s danou podstavou) nebo rotační kužele:
V=(Sp*v)/3
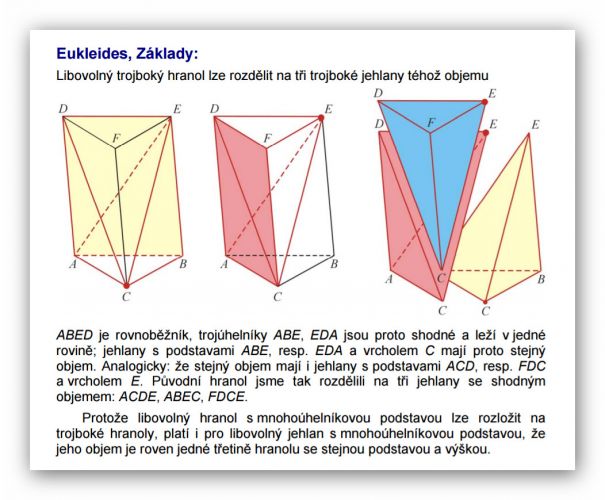
Zajímá mě, proč je ve vzorci zrovna číslo 3, tj. proč se do krychle či válce se shodnou podstavou a výškou vejdou zrovna tři jehlany či kužele? Lze to nějak vypočítat, nebo jde o konstantu?
0x
Asi jsi chtěl napsat kvádr a kužel. Ano jde to spočítat. Jako rozřežeš ten jehlan nebo kužel na destičky o výšce blížící se nule. Spočteš objem této destičky jako kvádr, nebo válec a pak sečteš objemy všech těchto destiček. Říká se tomu integrál od nuly po "v". K tomu ovšem musíš spočítat jak se v závislosti na výšce mění hrana, nebo průměr této destičky.
0x
kámo to bych chtěl vidět to tvý kádrový odvození...
Je to protože objem jehlanu nebo kuželu se dá spočítat např. integrací plošných řezů o ploše S(y) přes výšku y od 0 do h . Právě proto je dobrý příklad jehlan / kužel nebo jiné tělěso, které má nahoře špičku a dole libovolný 2D tvar (třeba siluetu clinta ýstvůda), plocha podstavy je S(h)=Š.
Objem je integrál od 0 do h z S(y) dy. S(y)= (y/h)^2 *Š (na druhou protože podstava se zmenšuje jak v délce tak šířce proporčně). a integrál z y^2 snad znáš.
doplněno 25.01.17 09:27:
no jo, jehlan zrovna jde... ale už nepůjde třeba nepravidelný 11úhelník touto metodou
0x
jj, odvozování objemů, známá a oblíbená disciplína z matematiky II. Integruješ plochu, čili druhou mocninu.
Si všimni. U dvojrozměrných tvarů máš ve jmenovateli dvojku. Když zinteguješ x, dostaneš x2/2, plocha trojúhelníka.
Přidej rozměr a dostaneš třírozměrný tvar a ve jmenovateli trojku x3/3, čili objem jehlanu o podstavě x krát x a výšce x.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.