Nejste přihlášen/a.
Prosím poradil by mi někdo, potřebuju vypočítat tento příklad na limitu (viz. obrázek - hořejšek zadání, výpočet v [] ), ale teď nevím jak postupovat dál, poradil by mi někdo.
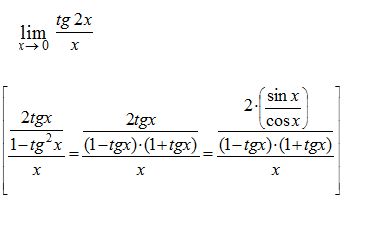
Nechápu, můžeš mi to blíže osvěstlit tu situaci. A jak mi to pomůže, když v zadádní mám tg2x v čitateli.
Zkusím, podmínku limity nepíšu
((sin 2x)/(cos 2x))/x * 2/2 =((sin 2x)/2x) * (2/(cos 2x)) = 2
Tangens upravíme na podíl, rozšíříme o zlomek 2/2 . Limita prvního členu je 1 a druhého 2
Poraď mi prosím, dopočítal jsem se až sem a nevím jak dál.
((sin2x)/(1+sinx*cosx)*(1-sinx*cosx))/x
Rozkládat goniometrické funkce můžeš do nekonečna, ale nevypořádáš se s X. Jsem si jist, že je nutno využít definovanou základní goniometrickou limitu. Řešení jsem nabídl
doplněno 20.01.17 22:31:
Tady se můžeš inspirovat
Příklad lze řešit ještě jednodušeji. Podle odkazu je i limita když x se blíží nule lim (tg x)/x = 1 lépe řečeno a platí i pro sinus (tg nx)/nx = 1 a proto upravujeme na tento tvar
Lim (tg 2x)/x = ((tg 2x)/x) * (2/2) = ((tg 2x)/2x) * (2/1) = 1 * 2 = 2
Nikde ten výraz v čitateli nevidím. Ve jmenovateli ano
Myslím že závorky jsou dost jasné a znak * je násobení dvou mnohočlenů. V rámci mnohočlenů je snad násobení jasné
Pokud nevíš že tg x = sin x/cos x, tg nx = sin nx/cos nx, tg 2x = sin 2x/cos 2x
Tak asi nemá cenu pokračovat
Na vzorečky jsem se koukal do tabulek a tam pro tg2x = (2tgx) / (1 - tg2x).
Lim (tg 2x)/x = ((tg 2x)/x) * (2/2) = ((tg 2x)/2x) * (2/1) = 1 * 2 = 2 A proč se zrovna rozšiřuje 2 - chápu aby jsem dostal ve jmenovateli 2x. Ale jaké je obecné pravidlo, kdy se má u lomenných výrazů použít rozšíření (1. když mám třeba zlomek = tak tomu se usměrnění, 2. jsou nějaké další?)
doplněno 20.01.17 23:32:
Tou lehčí metodu to už chápu jak si uvedl. A kdyby se to dělalo tou první metodou tak nechápu jak jsi dostatl do toho jmenovatele na začátku cos2x
2*(sinx*cosx/1) / (1-tgx)*(1+tgx) / x = (sin2x) / (1 - sinx/cosx)*(1+sinx/cosx) / x =
(sin2x) / (1 - sinx/1 * cosx/1) * (1 + sinx/1 * cosx/1) / x =
(sin2x) / (1+sinx*cosx)*(1-sinx*cosx) / x
K tomu jsem se dostal a nevím jak si tam dostal to cos2x. Poradíš mi prosím.
V těhlech výrazech ať budeš rozkládat jak chceš tak se nikdy nezbavíš x. Proto je potřeba využít předem definovanou limitu. Obecně pokud je u x koeficient tak na stejnou hodnotu musíme upravit i jmenovatele a pak platí limita
(Sin nx)/nx = 1
(tg nx)/nx = 1
Prostě to asi použijí tehdy pokud ve výrazu mimo goniometrickou hodnotu je i samostatná neznámá, v našem případě x
doplněno 20.01.17 23:38:
Přečti si příspěvek 22:56 snad dokážeš pochopit jak se nechá upravit tangens
tgx = sinx/cosx = sinx * cosx/1. No já vím, diť jsem ho tam použil.
doplněno 21.01.17 00:30: oprava tgx = sinx/cosx = sinx * 1/cosx . Ten druhý postup chápu. Ale ten první vůbec.Nechápu, jak si dostal do čitatele sin2x a ve jmenovateli cos2x. Mohl bys prosím uvést podrobnější postup výpočtu.(sin 2x)/(cos 2x))/x * 2/2 =((sin 2x)/2x) * (2/(cos 2x)) = 2
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.