Dobrý den, prosím poradil byste mi někdo prosím jak vyřešit tento příklad.
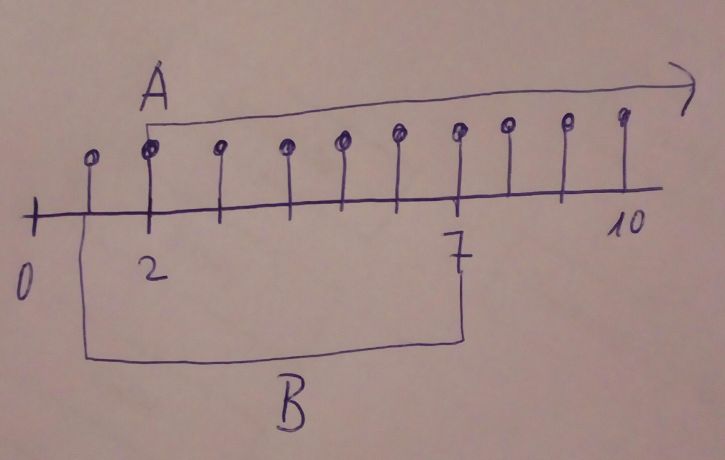
Zadání
A = {x € N; x> 2}
B = {x € N; x <7}
A´B =?
---------------
0x
Nejdřív si třeba množiny nakresli. Doplněk AB znamená, že prvky jsou v množině B, ale nejsou v množině A. V Tvém příkladě to bude jedno číslo...
Číslo 1?
A ještě v tomhle případě, když je to obor N - přirozená čísla, tak se množiny zakreslují pomocí výčtu prvků?, a nemělo by to býl namalovaný u A až od 3, když v zadání je> 2; a v B by to mělo být až od 6, podle mě, nejsem si jist, poradíš mi?
Kdyby to byly intervaly, tak by u 7 a u 2, byly prazdný kolečka u A a B (což lze malovat, když x € R, když je obor N - tak by intervali neměli jít malovat) Nemýlím se?
Promiň, spletla jsem se, ano měli by tam být nevyplněné tečky a výsledek bude {7,8,9,10...} - doplněk množiny B v množině A.
Množina přirozených čísel vypadá např. M = {1;5;6;12}. A ano, u přirozených čísel nejsou intervaly, jen se prvky zapisují pomocí množin.
Ještě, když jsi to nakreslim pomocí Venova diagramu,
tak u A to začíná od 2 nebo od 3 (když je tam> 2), a u B to začíná od 6 (když je tam <7)?
Mám správný výsledek - výsledek = {1; 2}? Jinak díky za rady.
doplněno 17.01.17 15:32:
Jo a ještě, jak by byl výsledek, kdyby šlo o R? Prosím poradíš mi.
Jakto, mě to přijde nějaké divné. Cituji z učebnice "Doplněk (komplement) množiny A v množině B tvoří všechny prvky, které patří do množiny B a nepatří do množiny A. Značíme A´B.
Např: A = { 1; 2; 3 } B = { 1; 2; 3; 4; 5 } A´B = { 4; 5 }"
V mém případě, tak jsem to pochopil dle textu z učebnice (zkráceně = prvky z B, které nepatří (nejsou obsaženy) do množiny A)
A = { 3; 4; 5; 6; 7; 8; 9; 10; 12; 13; 14; 15 ...}
B = { 6; 5; 4; 3; 2; 1}
A´B = { 2; 1 }
Nemýlím se?
Definici doplňku uvádíš správně, ale za předpokladu, že množina A je obsažena v množině B, tedy A ⊆ B. Pak doplňkem množiny A v množině B rozumíme množinu
A’B = B – A
Graficky můžeme doplněk množiny A v množině B znázornit následujícím diagramem:
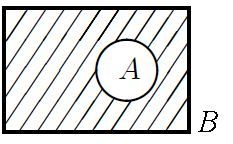
Nechápu. Jak to, že A je podmnožina B neplatí (jak na to přijdu, že to neplatí). A k čemu to potřebuji vědět. Když, já chci znát doplněk a ne podmnožinu. A jak z toho vyplívá že nelze vytvořit doplněk.
Mohl bys mi to prosím lépe vysvětlit, i další věci okolo množin, jestli jsou nějaké podmínky, či co.
Máme nějakou množinu, např. {5,8,10,12,15,20,21,22} a z ní vyjmu prvky {8, 10,15, 20, 21}. Z původní množiny zbudou prvky {5, 12, 22}. A tento zbytek se nazývá doplněk.
.
Najdi si v matematicko-fyzikálních tabulkách množinové pojmy. Jsou uvedeny hned na začátku tabulek.
V tvém zadání množina B neobsahuje prvky 7, 8 , 9 ... a tak je nemohu vyjmout. Jinak, abys mohl vytvořit doplněk, musí být množina A obsažena v množině B.
doplněno 17.01.17 21:35:
Zřejmě se má určit doplněk množin A, B v množině N.
A’N = N – A =?
B’N = N – B =?
Díky za rady.
A ještě, jak přišla elisa24 na: "Tak to bude jen {2}".
Takže tedy v tomto případě nejde tvořit A´B a ani naopak, B´A?
A ještě bych potřeboval poradit, co znamená toto (co se tím míní):
" Aby bylo možné doplněk definovat, je třeba znát množinu, vzhledem ke které se doplněk počítá. ( cs.wikipedia.org/..."
A⊆B (tohle vim = A je podmnožinou B), pak BC⊆AC (ale, tohle nevim) "?
A jaký je rozdíl mezi inkluzí a ostrou inkluzí (jestli jsem to pochopil, tak když mám ostrou inkluzi, tak můžu udělat v tomhle případě podmnožinu, a pak bych mohl i ten doplněk, ano?)?
doplněno 18.01.17 00:26:
A ještě jak by se postupovalo, to co si navrhl ty:
" Zřejmě se má určit doplněk množin A, B v množině N. (množina N, to se myslí základní množina U?)
A’N = N – A =?
B’N = N – B =?
"
0x
Ten tvůj odkaz by měl být takto:
Informace od @elisa24 nejsou správné. Sice správně uvádí "Doplněk A‘B znamená, že prvky jsou v množině B, ale nejsou v množině A."Ale zapomněla dodat, že množina A je podmnožinou B (A ⊂ B).
Doplněk (komplement) množiny je definován takto:
Je-li množina A podmnožinou B, pak doplňkem A’B rozumíme množinu všech prvků množiny B, které nejsou v množině A.
A ⊂ B ⇒ A’B = B – A
Vyšrafovaná část - viz obrázek výše.
.
Takže není-li množina A podmnožinou B, pak nemá smysl hovořit o doplňku množiny A v množině B.
.
Jaký je rozdíl mezi ostrou a neostrou inkluzi? Platí mezi nimi vztah podobný ostré a neostré nerovnosti (x <3 nebo x ≤ 3). Neostrá inkluze tedy rovnost připouští, ostrá nikoli. Chceme-li zapsat ostrou inkluzi, použijeme místo značky ⊆ značku ⊂.
.
N = {1, 2, 3, 4, 5, 6, 7, 8 ...} ... množina všech přirozených čísel
A = {x € N; x> 2} = {3, 4, 5, 6, 7, 8, 9 ...}
B = {x € N; x <7} = {1, 2, 3, 4, 5, 6}
.
A’N = N – A = {1, 2}
B’N = N – B = {7, 8, 9 ...} = {x € N; x> 6}
Pokud A⊆B, pak BC⊆AC (čerpáno z cs.wikipedia.org/...
)
= znamená to samé - to co jsi napsal (ano nebo ne, případně jestli bys mi to prosím vysvětlil) A ⊂ B ⇒ A’B= B – A?
A jde z mého zadání udělat ostrou inkluzi (ostrou podmnožinu), ano či ne?
A šlo by teda udělat B´A?
Jinak, díky moc za ochotu.
Značení se u různých autorů různí. V tvém odkazu značí doplněk A C . Ty ho značíš A‘. Někde ho značí pruhem nad A ( http://www.matematika.cz/mnozinove-operace ).
Tento tvůj zápis "Pokud A⊆B, pak B C ⊆A C " je nesmysl. Jestliže je A podmnožinou B a doplněk B‘ (čili B C ) neexistuje.
Zde máš odkazy, kde jsou vysvětleny množinové pojmy:
http://kdm.karlin.mff.cuni.cz/diplomky/moravecdp/mnoziny.php
http://www.matematika.cz/mnozinove-operace
A zde je video:
Šlo by teda udělat B je podmnožinou A z mého zadání, i když množina B má navíc na 2 prvky a to čílo 1 a 2, které množina A nemá?
A šlo by teda udělat B´A?
A = { 3; 4; 5; 6; 7; 8; 9; 10; 12; 13; 14; 15 ...}
B = { 6; 5; 4; 3; 2; 1}
Nešlo. Množina B není podmnožinou množiny A. I v tom videu hned na začátku říká, že doplněk lze utvořit pouze v případě, že množina B je podmnožinou A.
.
Doplněk B’A je ta vyšrafovaná část:
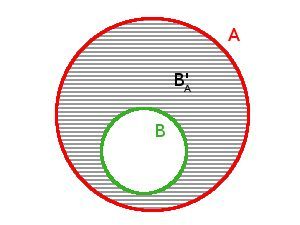
Takže, jestli to chápu tak když má "podmožina" prvky navíc, která množina nemá, tak to není podmnožina?V mém případě 1 a 2 jsou navíc. Je to tak?
Zkrátka musí podmnožina obsahovat prvky, která obsahuje hlavní množina a žádné navíc, které hlavní množina nemá, je to tak?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.