Nejste přihlášen/a.
1x
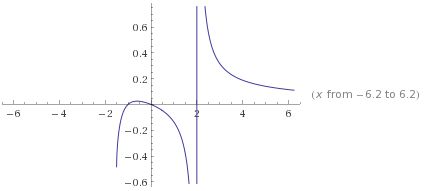
Je to přímé dosazení. Tam snad nejde nic zkazit. Bod -1 je pro tu funkci nezajímavý. Bod -2 by byl mnohem zajímavější.
Proč je tam druhý způsob výpočtu, to nevím.
doplněno 10.01.17 02:19:
Oprava: Bod -1 je pro tu funkci nezajímavý z hlediska spojitosti funkce. Jinak samozřejmě ten bod je ještě s bodem x=0 významný tím, že v něm funkce nabývá nulové hodnoty. (Dalším nulovým bodem je nekonečno, což se v některých případech také může hodit).
Nejdříve díky moc za odpověď ...
Viděla jsem podíl ... -> vyučující nám doporučovali - když uvidíte podíl - zkuste využít L´Hospit. pravidlo ... -> pokus o využití L´Hosp. pravidla ...dosazení hodnoty x -> -1 do výrazu => výsledek 0 / -3 nikoli 0/0 nebo nekonečno / nekonečno ... a tudíž ten další rozklad (roznásobování odmocnin)... pro jistotu ...
Ještě jednou díky
Žádné použití LHospitalova pravidla (=derivace vršku a spodku) tam nevidím a ani by nebylo zapotřebí, když zlomek po dosazení nevychází 0/0 nebo inf/inf.
Je vidět, že limita ve spojitém bodě funkce je prostě jen funkční hodnota v tom bodě a proto nejsou zapotřebí žádné "triky" a pravidla vyučovaná pro počítání limit v nespojitých bodech.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
